(Solved): Angular Momentum Analysis Master equation: Equation for this situation: Questions 1. Percent error ...

Angular Momentum Analysis Master equation: Equation for this situation: Questions 1. Percent error acceleration 2. Percent error velocity 3. Percent error velocity 4. Error comparison Report Sheet The Rolling Can Remember to complete all calculations in $\mathrm{kg},\mathrm{m},\mathrm{s},\mathrm{N}$ and $\mathrm{J}!$ Also include complete calculations: equation, numbers in equation, answer with a unit. Data: Can mass: $.425\mathrm{kg}$ Can diameter: $.08\mathrm{m}$ Can radius: $.04\mathrm{m}$ Ramp length: $.76m$ Ramp height: $.04\mathrm{m}$ Level surface distance: $.76\mathrm{m}$ Trial 2 Trial $3$ Average Time on the ramp: $\frac{2.83}{3.02}?3.26$ 2.97 Time on level surface: 4.61 4.68 4.78 4.69 $\sec$ Calculate the following Torque: Moment of inertia: Angular acceleration Translational acceleration 1) Moment of Inertia (I) $\begin{array}{l}I=\frac{1}{2}m{r}^2[\text{ fon rolling can/dise] }\\ I=\frac{1}{2}\times 0.425\times (0.04{)}^2\\ I=3.4\times 10^{?4}\mathrm{Kg}?{\mathrm{m}}^2\end{array}$ 2) Translational aculeration (a). 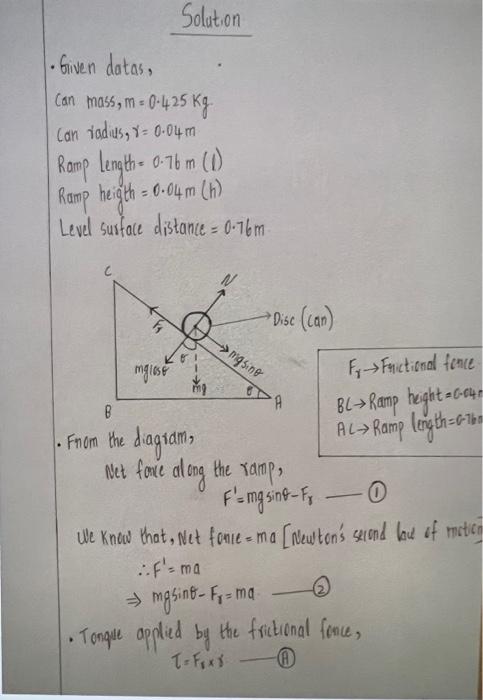From equation (4), $a=\frac{2}{3}g\sin ?.$ From equation (5), $\begin{array}{c}\sin ?=0.052\\ a=\frac{2}{3}\times 9.81\times 0.052\\ a=0.340\mathrm{m}/{\mathrm{s}}^2\end{array}$ 3) Angular accelecation $(?)$ $?=\frac{a}{?}=\frac{0.340}{0.04}$ - Given datas, can mass, $m=0.425\mathrm{kg}$. Can iadus, $?=0.04\mathrm{m}$ Ramp length $=0.76\mathrm{m}(1)$ Ramp height $=0.04\mathrm{m}(\mathrm{h})$ Level surfoce distance $=0.76\mathrm{m}$ - Fnom the diagram, Net fance al ong the ramp, $F^{?}=mg\sin ??F_r?\text{ ( ) }$ We know that, Net fanie = ma [Newten's selend law if motien $\begin{array}{l}?F^{?}=ma\\ ?mg\sin ??F_r=ma\end{array}$ - Tonque applied by the frictional fince, $T=F_1\times i_{\text{O }}$ (II) But, $?=I\times ?I?$ moment of inertia also, $a=?xr$ $\begin{array}{c}?=\frac{d}{?}\\ ??=\frac{Ia}{?}\text{ (B) }\end{array}$ comparing equation (A) and (B), We $g\left(t,\frac{Ia}{r}=F_{rr}\right)$ - For the disc, $I=\frac{1}{2}m{r}^2$ [Fon can dse] $\text{ So, }\begin{array}{l}\frac{m{?}^{2}a}{2?}=F_{?}x\\ ?F_{?}=\frac{ma}{2}?\text{ (3) }\end{array}$ (omparing equations (2) and (3), We get, $mg\sin ??\frac{ma}{2}=ma$ $\begin{array}{rl}& g\sin ?=\frac{3}{2}a\\ ?& a=\frac{2}{3}g\sin ?\end{array}$ - Fnom the figure,