(Solved): An overhang beam as shown in Figure 1 is simply supported at A and B and is subjected to a ...

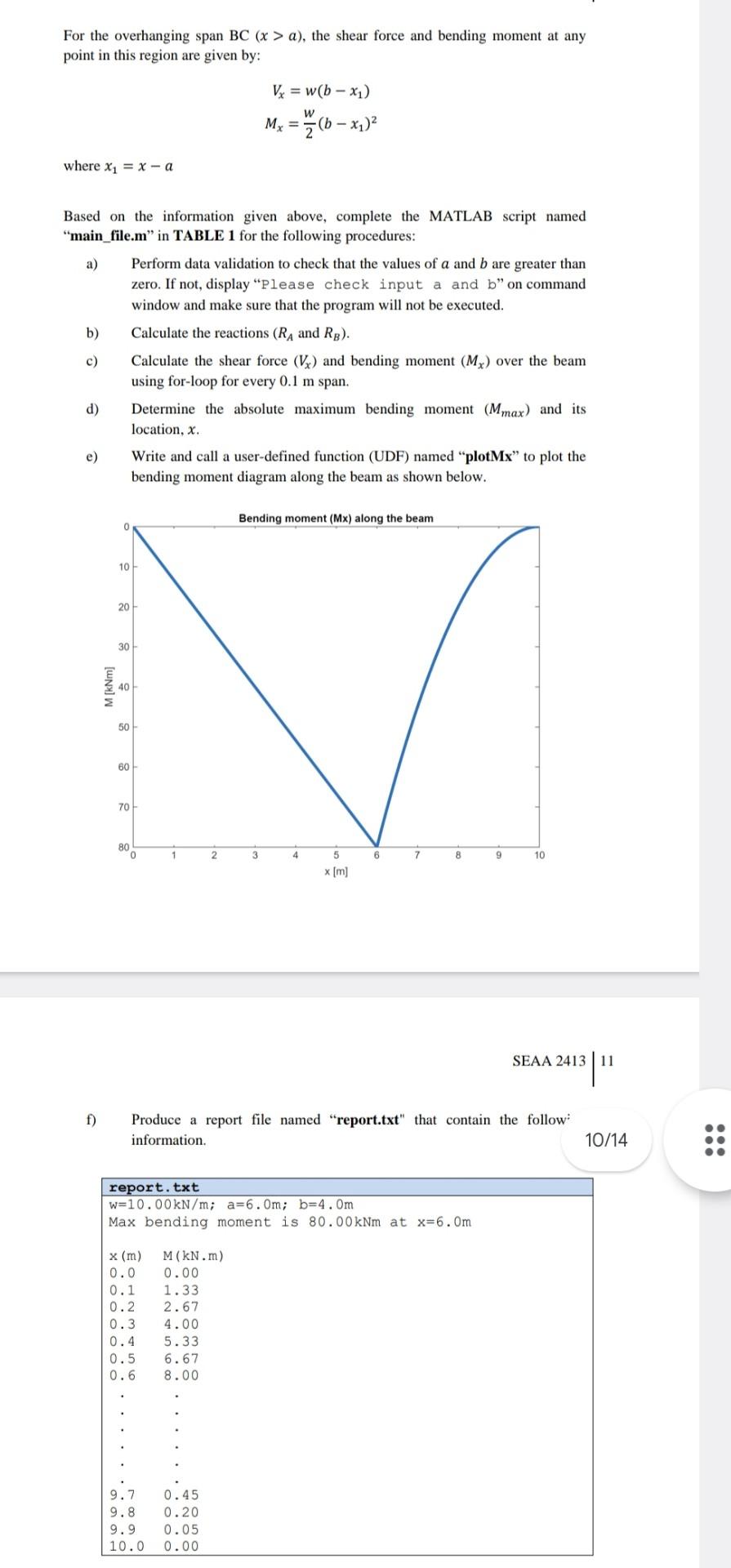
An overhang beam as shown in Figure 1 is simply supported at $A$ and $B$ and is subjected to a uniformly distributed load (UDL) $(w)$ over the overhanging span BC. The reaction at supports can be calculated as: $\begin{array}{c}{R}_A=\frac{w{b}^2}{2a}\\ R_B=wb+R_A\end{array}$ where $a$ is the simply supported span $\mathrm{AB}$ and $b$ is the length of overhanging region BC. For the simply supported span $\mathrm{AB}(x?a)$, the shear force and bending moment at any point in this region are given by: $\begin{array}{c}{V}_x=?R_A\\ M_x=R_A\times x\end{array}$ SEAA 2413 For the overhanging span $\mathrm{BC}(x>a)$, the shear force and bending moment at any point in this region are given by: $\begin{array}{rl}{V}_x& =w\left(b?x_1\right)\\ M_x& =\frac{w}{2}{\left(b?x_1\right)}^2\end{array}$ where $x_1=x?a$ Based on the information given above, complete the MATLAB script named "main_file.m" in TABLE 1 for the following procedures: a) Perform data validation to check that the values of $a$ and $b$ are greater than zero. If not, display "Please check input $a$ and b" on command window and make sure that the program will not be executed. b) Calculate the reactions $(R_A$ and $R_B)$. c) Calculate the shear force $\left(V_x\right)$ and bending moment $\left(M_x\right)$ over the beam using for-loop for every $0.1\mathrm{m}$ span. d) Determine the absolute maximum bending moment $\left(M_{\max }\right)$ and its location, $x$. e) Write and call a user-defined function (UDF) named "plotMx" to plot the bending moment diagram along the beam as shown below. For the overhanging span $\mathrm{BC}(x>a)$, the shear force and bending moment at any point in this region are given by: $\begin{array}{rl}{V}_x& =w\left(b?x_1\right)\\ M_x& =\frac{w}{2}{\left(b?x_1\right)}^2\end{array}$ where $x_1=x?a$ Based on the information given above, complete the MATLAB script named "main_file.m" in TABLE 1 for the following procedures: a) Perform data validation to check that the values of $a$ and $b$ are greater than zero. If not, display "Please check input a and b" on command window and make sure that the program will not be executed. b) Calculate the reactions $(R_A$ and $R_B)$. c) Calculate the shear force $\left(V_x\right)$ and bending moment $\left(M_x\right)$ over the beam using for-loop for every $0.1\mathrm{m}$ span. d) Determine the absolute maximum bending moment $\left(M_{\max }\right)$ and its location, $x$. e) Write and call a user-defined function (UDF) named "plotMx" to plot the bending moment diagram along the beam as shown below. SEAA 2413 11 f) Produce a report file named "report.txt" that contain the follow: information. $10/$