Home /
Expert Answers /
Advanced Physics /
an-infinite-uniform-plane-charge-of-surface-charge-density-cuts-through-a-spherical-gaussian-su-pa123
(Solved): An infinite, uniform plane charge of surface charge density cuts through a spherical Gaussian su ...
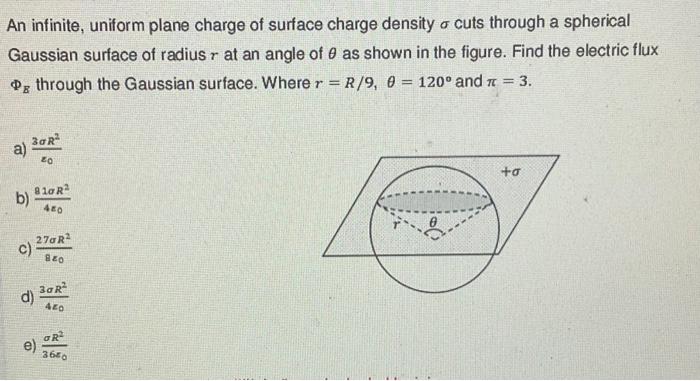
An infinite, uniform plane charge of surface charge density cuts through a spherical Gaussian surface of radius at an angle of as shown in the figure. Find the electric flux through the Gaussian surface. Where and . a) b) c) d) e)
Expert Answer
To find the electric flux through the Gaussian surface, we need to apply Gauss's law, which relates the electric flux through a closed surface to the charge enclosed within that surface:? = q/?0 where ? is the electric flux through the surface, q is the charge enclosed within the surface, and ?0 is the electric constant.In this problem, we have an infinite, uniform plane charge of surface charge density ? cutting through a spherical Gaussian surface of radius r at an angle of ?, where r = R/9 and ? = 120°. We need to find the electric flux through this Gaussian surface.To apply Gauss's law, we need to find the charge enclosed within the Gaussian surface. The charge enclosed within a Gaussian surface is equal to the product of the surface charge density and the area of the surface. The surface area of a sphere is given by:A = 4?r^2 where r is the radius of the sphere.In this problem, the surface area of the spherical Gaussian surface is:A = 4?r^2 = 4?(R/9)^2 = (4?R^2)/81The charge enclosed within the Gaussian surface is:q = ?A = ?(4?R^2)/81