(Solved): An exponential function f(x)=abx passes through the points (0,6) and (3,384). What are the value ...

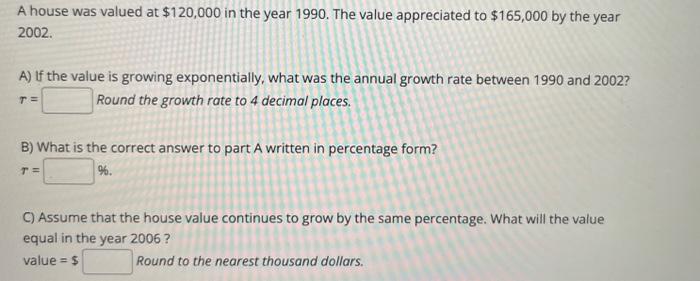
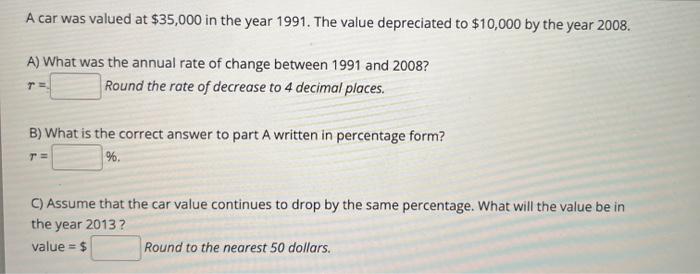
An exponential function $f(x)=a?b^x$ passes through the points $(0,6)$ and $(3,384)$. What are the values of $a$ and $b$ ? $a=\text{ and }b=$ An exponential function $f(x)=a?b^x$ passes through the points $(0,11000)$ and $(2,3960)$. What are the values of $a$ and $b$ ? $a=\text{ and }b=$ Find a formula for the exponential function passing through the points $\left(?3,\frac{1}{2}\right)$ and $(2,16)$ $f(x)=$ A radioactive substance decays exponentially. A scientist begins with 110 milligrams of a radioactive substance. After 14 hours, $55\mathrm{mg}$ of the substance remains. How many milligrams will remain after 19 hours? $\mathrm{mg}$ Give your answer accurate to at least one decimal place A house was valued at $\$120,000$ in the year 1990 . The value appreciated to $\$165,000$ by the year 2002. A) If the value is growing exponentially, what was the annual growth rate between 1990 and $2002?$ $r=$ Round the growth rate to 4 decimal places. B) What is the correct answer to part A written in percentage form? $r=$ $\%$. C) Assume that the house value continues to grow by the same percentage. What will the value equal in the year 2006 ? value $=\$$ Round to the nearest thousand dollars. A car was valued at $\$35,000$ in the year 1991 . The value depreciated to $\$10,000$ by the year 2008 . A) What was the annual rate of change between 1991 and 2008? $r=$ Round the rate of decrease to 4 decimal places. B) What is the correct answer to part A written in percentage form? $r=$ $\%$. C) Assume that the car value continues to drop by the same percentage. What will the value be in the year 2013? value $=\$$ Round to the nearest 50 dollars. 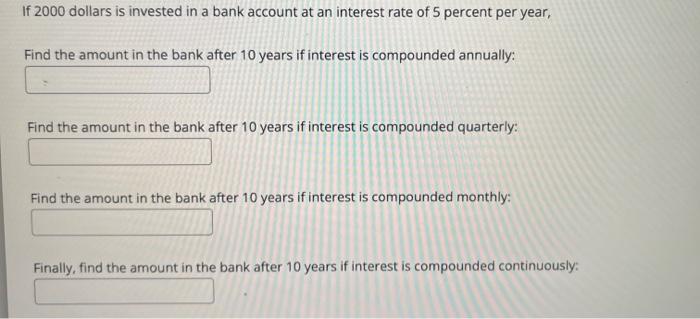If 2000 dollars is invested in a bank account at an interest rate of 5 percent per year, Find the amount in the bank after 10 years if interest is compounded annually: Find the amount in the bank after 10 years if interest is compounded quarterly: Find the amount in the bank after 10 years if interest is compounded monthly: Finally, find the amount in the bank after 10 years if interest is compounded continuously: 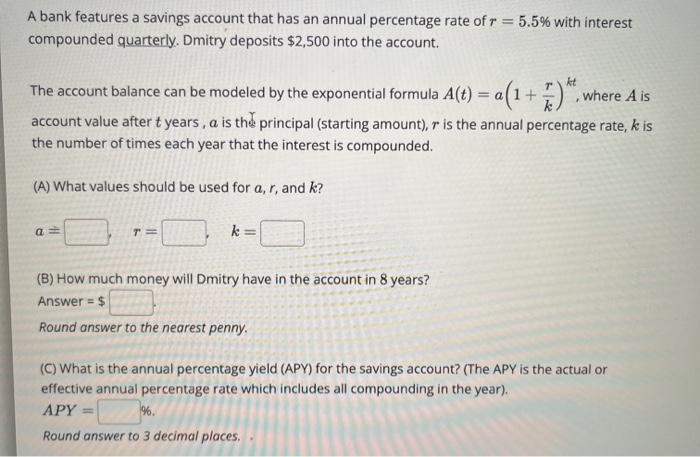A bank features a savings account that has an annual percentage rate of $r=5.5\%$ with interest compounded quarterly. Dmitry deposits $\$2,500$ into the account. The account balance can be modeled by the exponential formula $A(t)=a{\left(1+\frac{r}{k}\right)}^{kt}$, where $A$ is account value after $t$ years, $a$ is the principal (starting amount), $r$ is the annual percentage rate, $k$ is the number of times each year that the interest is compounded. (A) What values should be used for $a,r$, and $k$ ? $a=r=k=$ (B) How much money will Dmitry have in the account in 8 years? Answer $=\$$ Round answer to the nearest penny. (C) What is the annual percentage yield (APY) for the savings account? (The APY is the actual or effective annual percentage rate which includes all compounding in the year). $APY=$ $\%$. Round answer to 3 decimal places. 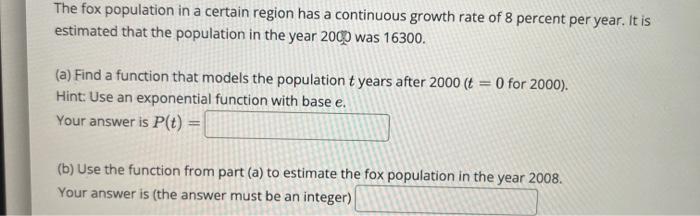The fox population in a certain region has a continuous growth rate of 8 percent per year. It is estimated that the population in the year 2000 was 16300. (a) Find a function that models the population $t$ years after 2000 ( $t=0$ for 2000$)$. Hint: Use an exponential function with base $e$. Your answer is $P(t)=$ (b) Use the function from part (a) to estimate the fox population in the vear 2008. Your answer is (the answer must be an integer) A population of bacteria is growing according to the equation $P(t)=1450e^{0.1t}$, Estimate when the population will exceed 2062. Give your answer accurate to one decimal place. 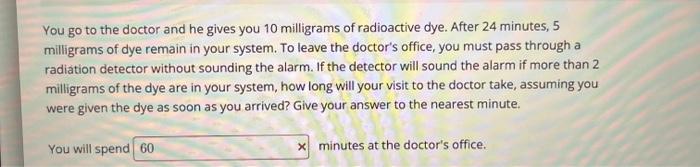You go to the doctor and he gives you 10 milligrams of radioactive dye. After 24 minutes, 5 milligrams of dye remain in your system. To leave the doctor's office, you must pass through a radiation detector without sounding the alarm. If the detector will sound the alarm if more than 2 milligrams of the dye are in your system, how long will your visit to the doctor take, assuming you were given the dye as soon as you arrived? Give your answer to the nearest minute. You will spend minutes at the doctor's office. 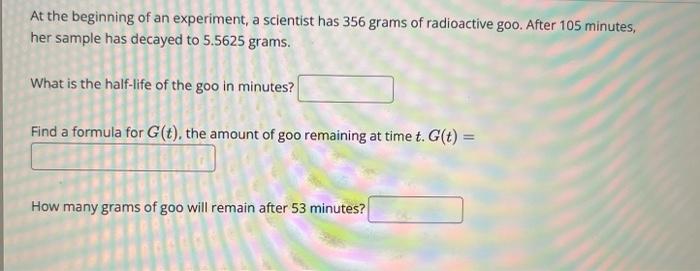At the beginning of an experiment, a scientist has 356 grams of radioactive goo. After 105 minutes, her sample has decayed to 5.5625 grams. What is the half-life of the goo in minutes? Find a formula for $G(t)$, the amount of goo remaining at time $t.G(t)=$ How many grams of goo will remain after 53 minutes? A wooden artifact from an ancient tomb contains 20 percent of the carbon-14 that is present in living trees. How long ago, to the nearest year, was the artifact made? (The half-life of carbon-14 is 5730 years.) years. 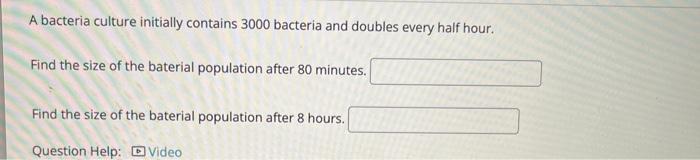A bacteria culture initially contains 3000 bacteria and doubles every half hour. Find the size of the baterial population after 80 minutes. Find the size of the baterial population after 8 hours. Question Help: [b Video The count in a bacteria culture was 600 after 15 minutes and 1400 after 30 minutes. Assuming the count grows exponentially, What was the initial size of the culture? bacteria Find the doubling period. minutes Find the population after 85 minutes. bacteria When will the population reach 14000 . minutes