(Solved): An electron in an infinite potential well is described by the following wavefunction: \[ \Psi(x)=\ ...

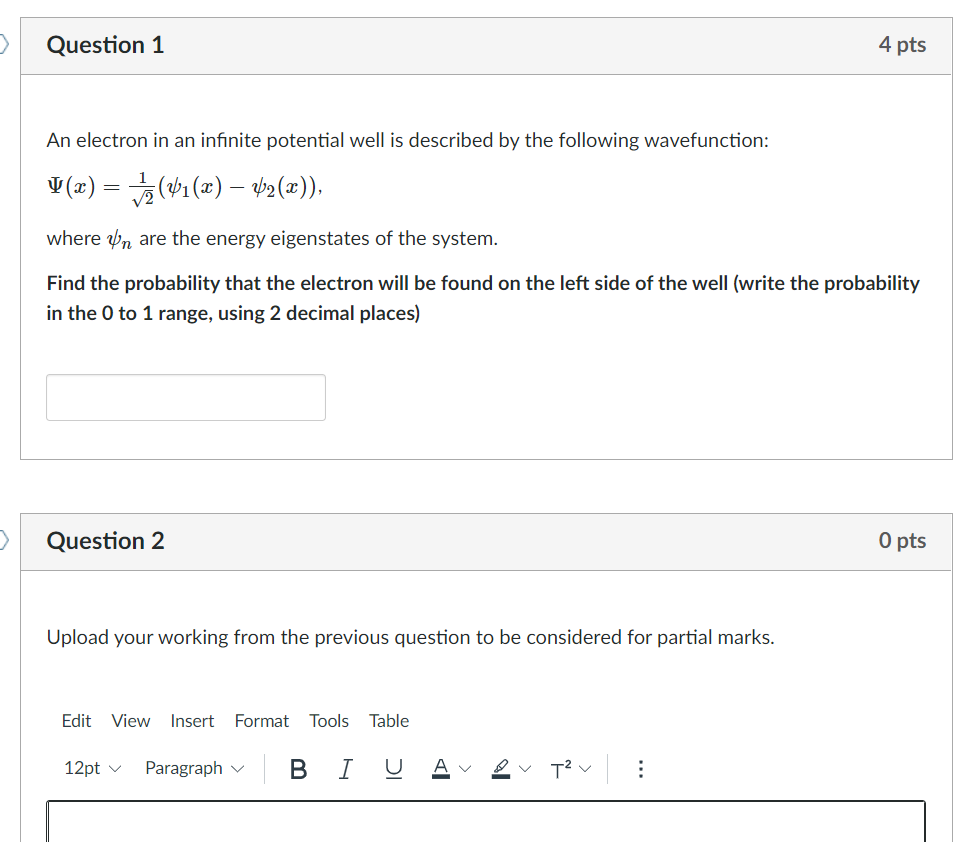
An electron in an infinite potential well is described by the following wavefunction: \[ \Psi(x)=\frac{1}{\sqrt{2}}\left(\psi_{1}(x)-\psi_{2}(x)\right) \] where \( \psi_{n} \) are the energy eigenstates of the system. Find the probability that the electron will be found on the left side of the well (write the probability in the 0 to 1 range, using 2 decimal places) Question 2 0 pts Upload your working from the previous question to be considered for partial marks.