(Solved): All four parts of this question refer to the following scrabble tiles. You do not need to understa ...

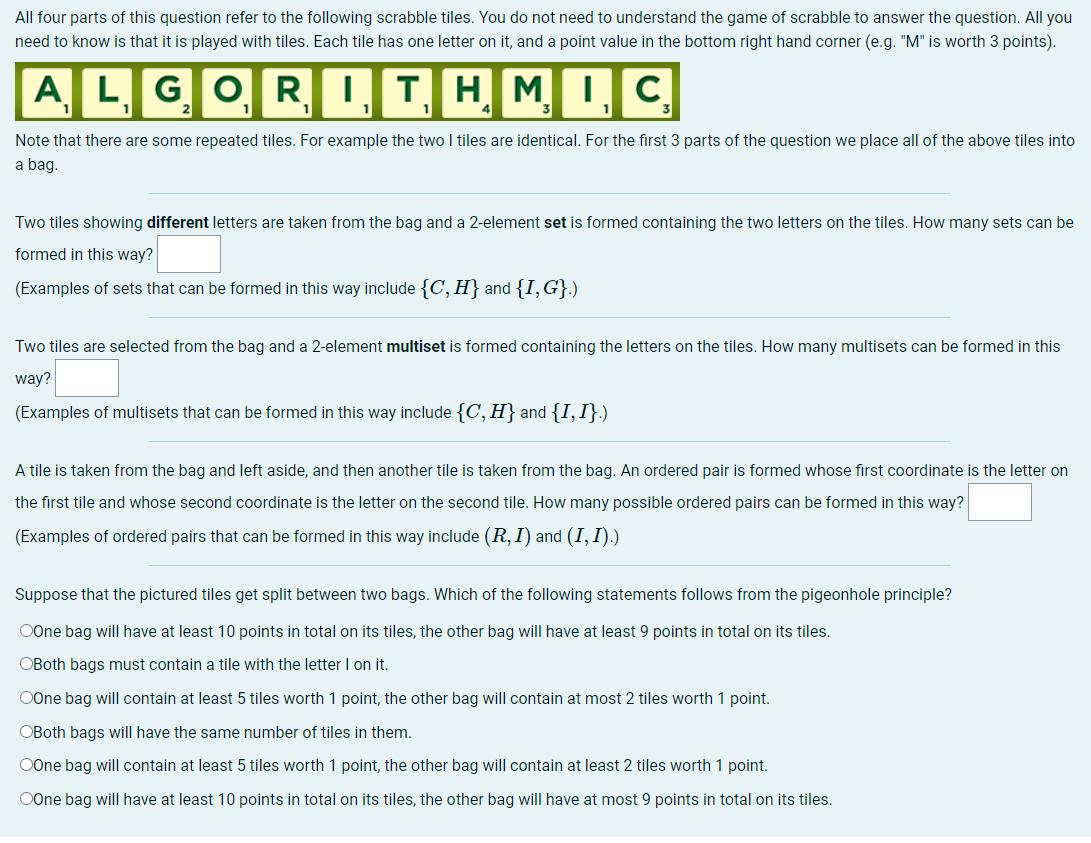
All four parts of this question refer to the following scrabble tiles. You do not need to understand the game of scrabble to answer the question. All you need to know is that it is played with tiles. Each tile has one letter on it, and a point value in the bottom right hand corner (e.g. "M" is worth 3 points). Note that there are some repeated tiles. For example the two I tiles are identical. For the first 3 parts of the question we place all of the above tiles into a bag. Two tiles showing different letters are taken from the bag and a 2-element set is formed containing the two letters on the tiles. How many sets can be formed in this way? (Examples of sets that can be formed in this way include \( \{C, H\} \) and \( \{I, G\} \).) Two tiles are selected from the bag and a 2-element multiset is formed containing the letters on the tiles. How many multisets can be formed in this way? (Examples of multisets that can be formed in this way include \( \{C, H\} \) and \( \{I, I\} \).) A tile is taken from the bag and left aside, and then another tile is taken from the bag. An ordered pair is formed whose first coordinate is the letter on the first tile and whose second coordinate is the letter on the second tile. How many possible ordered pairs can be formed in this way? (Examples of ordered pairs that can be formed in this way include \( (R, I) \) and \( (I, I) \).) Suppose that the pictured tiles get split between two bags. Which of the following statements follows from the pigeonhole principle? One bag will have at least 10 points in total on its tiles, the other bag will have at least 9 points in total on its tiles. Both bags must contain a tile with the letter I on it. One bag will contain at least 5 tiles worth 1 point, the other bag will contain at most 2 tiles worth 1 point. Both bags will have the same number of tiles in them. One bag will contain at least 5 tiles worth 1 point, the other bag will contain at least 2 tiles worth 1 point. One bag will have at least 10 points in total on its tiles, the other bag will have at most 9 points in total on its tiles.