(Solved): Advanced Physics We calculate thermal conductivity using Lee's method in this experiment. Plot on gr ...

Advanced Physics

We calculate thermal conductivity using Lee's method in this experiment.
Plot on graph paper the graphs between Time and Temperature for two different materials i.e.,
Bakelite and cardboard.
Obtain the slope from the graph for Bakelite and cardboard from the graph. ? Using the value of from graph and others parameters used in the formula, ((d*theta)/(dt)) ((d*theta)/(dt))

obtain the thermal conductivity K.

 

 

 

 

 

Measurement of Thermal Conductivity by Lee's method Object: To determine thermal conductivity of a bad conductor (bakelite/cardboard) in form of a disc using Lee's method. Apparatus: (1) Lee's apparatus and the experimental specimen in the form of a disc. (2) Two thermometers, (3) Stop watch, (4) Weighing balance, (5) Special lamp stand (6) Boiler (Cooker) and (7) Heater (Induction Stove) Theory: Thermal conductivity, k, is the property of a material that indicates its ability to conduct heat. Conduction will take place if there exists a temperature gradient in a solid (or stationary fluid) medium. Energy is transferred from more energetic to less energetic molecules when neighboring molecules collide. Conductive heat flow occurs in direction of the decreasing temperature because higher temperature is associated with higher molecular energy. Fourier's Law expresses conductive heat transfer as H = KA (T2-T1) X where H is the steady state rate of heat transfer, k is the thermal conductivity of the sample, A is the cross sectional area and (T2- T?) is the temperature difference across the sample thickness 'x' (see Fig. 1), assuming that the heat loss from the sides of the sample is negligible. To keep the loss from the sides small, the sample is made in form of a thin disk with a large cross sectional area compared to the area exposed at the edge. Keeping 'A' large and 'x' small produces a large rate of energy transfer across the sample. Keeping x small also means that the apparatus reaches a Fig. 1 steady state(when temperature T? and T? are constant) more quickly. H = KA (T?-T1) X H = KA (T2-T1) X (1) Generally speaking, there are a number of possibilities to measure thermal conductivity, each of them being suitable for a limited range of materials, depending on the thermal properties and the medium temperature. The most commonly used methods are Searle's method and Lee's disc method, for good and bad conductors of heat, respectively. In the experiment, we will use Lee's disc method to determine the thermal conductivity of a bad conductor, e.g. Glass. Description of Lee's apparatus: The apparatus shown in Fig. 2 consists of two parts. The lower part C is circular metal disc. The experimental specimen G, usually rubber, glass or ebonite (here it is glass) is placed on it. The diameter of G is equal to that of C and thickness is uniform throughout. A steam chamber is placed on C. The lower part of the steam chamber, B is made of a thick metal plate the same diameter as of C. The upper part is a hollow chamber in which two side tubes are provided for inflow and outflow of steam. Two thermometers T? and T? are inserted into two holes in C and B, respectively. There are three hooks attached to C. The complete setup is suspended from a clamp stand by attaching threads to these hooks. Steam in Glass disc (G) T? T1 Steam Chest Brass Base B Brass Disk C Fig.2 X Steam Out Photograph of thermal conductivity measurement setup When steam flows for some time, the temperatures recorded (T? and T?) gradually remain steady. This is the steady state. Let at the steady state, temperature of C = T?. Temperature of B = T?. Surface area of G = A Conductivity of G = k Thickness of G = x Hence amount of heat flowing through G per second, H is given by Eq. (1). When the apparatus is in steady state (temperatures T? and T? constant), the rate of heat conduction into the brass disc C is equal to the rate of heat loss from the bottom of it. The rate of heat loss can be determined by measuring how fast the isc C cools at the previous (steady state) temperature T? (with the top of the brass disk covered with insulation). If the mass and specific heat of the lower disc are m and s, respectively and the rate of cooling at T? is dT/dt then the amount of heat radiated per second is, Equating (1) and (2) and simplifying, k can be determined as, dT .(3) k = Msx A (T1-T?) dt, H = Ms dT dt = Msx dT nr² (T?-T?) dt Formula Used: Msx k = (7) ?r² (T?-T?) Where k is the thermal conductivity of the material M is the mass of the Lee's disc-0.964Kg S is the specific heat of the Lees's disc-0.49x 10³ Cal/Kg K x is the thickness the card board disc/glass disc/Bakelite disc T? is the steady temperature of the steam (100°C) T2 is the steady temperature of the disc r is the radius of the disc is the temperature gradient Procedure: 1. Fill the boiler with water to nearly half and heat it to produce steam. 2. In the mean time, take weight of C by a weighing balance. Note its specific heat from a constant table. Measure the diameter of the specimen by a scale or slide calipers, if possible. Calculate the surface area, A = ?r². 3. Measure the thickness of the specimen by screw gauge. Take observations at 5 spots and take the mean value. 4. Put the specimen, steam chamber etc. in position and suspend it from the clamp stand. Insert the thermometer. Check if both of them are displaying readings at room temperature. If not, note the difference 0, is to be added to (T2-T?) later. 5. Now stem is ready. Connect the boiler outlet with the inlet of the steam chamber by a rubber tube. 6. Temperatures recorded in the thermometers will show a rise and finally will be steady at T? and T?. 7. Wait for 10 minutes and note the steady temperature. Stop the inflow of steam. 8. Remove the steam chamber and the specimen G. C is still suspended. Heat C directly by the steam chamber till its temperature is about T? +7°. 9. Remove the steam chamber and wait for 2-3 minutes so that heat is uniformly distributed over the disc C. 10. Place the insulating material on C. Start recording the temperature at 2 minute intervals. Continue till the temperature falls by 10? from T?. 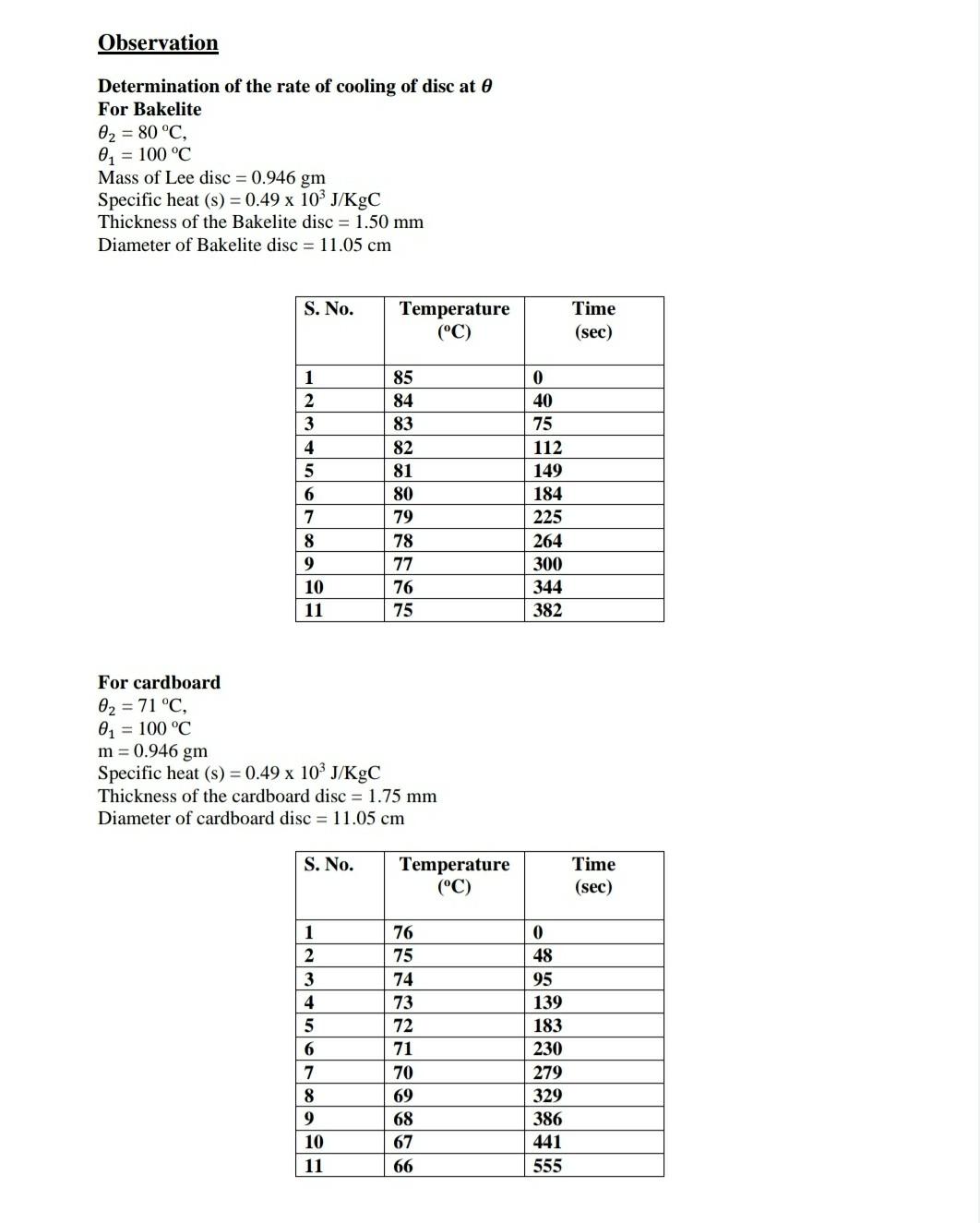Observation Determination of the rate of cooling of disc at For Bakelite 0? = 80 °C, 0? = 100 °C Mass of Lee disc = 0.946 gm Specific heat (s) = 0.49 x 10³ J/KgC Thickness of the Bakelite disc = 1.50 mm Diameter of Bakelite disc = 11.05 cm For cardboard 0? = 71 °C, 0? = 100 °C m = 0.946 gm S. No. 1 2 3 4 5 6 7 8 9 10 11 S. No. 1 2 Specific heat (s) = 0.49 x 10³ J/KgC Thickness of the cardboard disc = 1.75 mm Diameter of cardboard disc = 11.05 cm 3 4 5 6 7 8 9 M0ool- Temperature (°C) 10 11 85 84 83 82 81 80 79 78 77 76 75 Temperature (°C) 76 75 74 73 72 71 70 69 68 67 66 0 40 75 112 149 184 225 264 300 344 382 0 48 95 139 183 230 279 329 386 441 555 Time (sec) Time (sec)