(Solved): (a) Using a \( 0.05 \) level of significance, do students perform differently on the three areas of ...

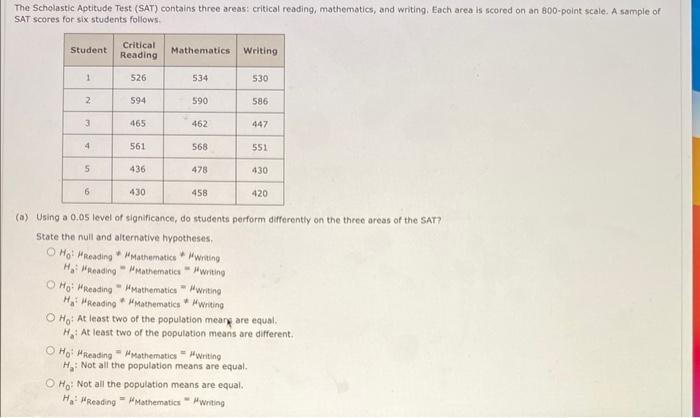
(a) Using a \( 0.05 \) level of significance, do students perform differently on the three areas of the SAT? State the null and alternative hypotheses. \( H_{0}: \) H\( _{\text {Reading }} \) * M Mathematics * M Wraing \( H_{0}: \mu_{\text {Reading }}=\mu_{\text {Mathematics }}=\mu_{\text {Writing }} \) \( H_{\text {a }} \) : \( H_{\text {feading }} \) * HMathematics * HWnting \( H_{0} \) : At least two of the population meary are equal. \( H_{a}: \) At least two of the population means are different. \( H_{0}: \mu_{\text {fieading }}=\mu_{\text {Mathematics }}=\mu_{\text {Writing }} \) \( H_{2} \) : Not all the population means are equal. \( H_{0} \) : Not all the population means are equal. \( H_{a}: \mu_{\text {Reading }}=\mu_{\text {Mathematics }}=\mu_{\text {wring }} \) Find the value of the test statistic. (Round your answer to two decimal places.) Find the p-value. (Round your answer to three decimal places.) \[ p \text {-value = } \] State your conclusion. Do not reject \( H_{0} \). There is not sufficient evidence to conclude that the mean scores for the three parts of the SAT are not all equal. Do not reject \( \mathrm{H}_{0} \). There is sufficient evidence to conciude that the mean scores for the three parts of the SAT are not all equal. Reject \( H_{0} \). There is not sufficient evidence to conclude that the mean scores for the three parts of the SAT are not all equal. Reject \( H_{0} \). There is sufficlent evidence to conclude that the mean scores for the three parts of the SAT are not all equal. b) Which area of the test seems to give the students the most trouble? Explain. The mean test scores for the three sections are for critical reading. for mathematics, and section has the lowest average score, this section appears to give the students the most trouble.