(Solved): A turboprop engine consists of a diffuser, compressor, combustor, turbine, and nozzle. The turbine ...

A turboprop engine consists of a diffuser, compressor, combustor, turbine, and nozzle. The turbine drives a propeller as well as the compressor. Air enters the diffuser with a volumetric flow rate of \( 63.7 \mathrm{~m}^{3} / \mathrm{s} \) at \( 40 \mathrm{kPa}, 240 \mathrm{~K} \), and a velocity of \( 180 \mathrm{~m} / \mathrm{s} \), and decelerates essentially to zero velocity. The compressor pressure ratio is 11 and the compressor has an isentropic efficiency of \( 85 \% \). The turbine inlet temperature is \( 1140 \mathrm{~K} \), and its isentropic efficiency is \( 85 \% \). The turbine exit pressure is \( 50 \mathrm{kPa} \) and the nozzle exit pressure is \( 40 \mathrm{kPa} \). Flow through the diffuser and nozzle is isentropic. Use an air-standard analysis and neglect kinetic energy except at the diffuser inlet and the nozzle exit. Step 1 Your answer is incorrect. Determine the power delivered to the propeller, in MW. \[ \dot{W}_{\text {prop }}= \] \[ \text { MW } \] Hint Attempts: unlimited Step 2 The parts of this question must be completed in order. This part will be available when you complete the part above. 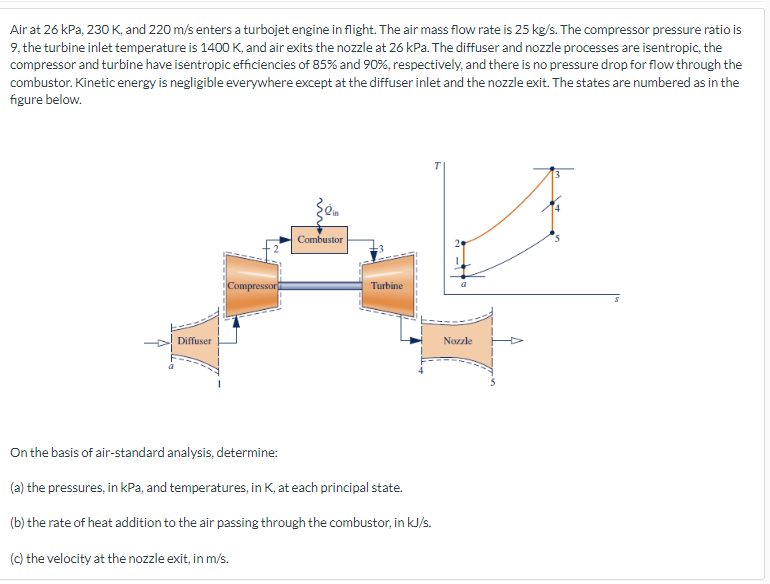Air at \( 26 \mathrm{kPa}, 230 \mathrm{~K} \), and \( 220 \mathrm{~m} / \mathrm{s} \) enters a turbojet engine in flight. The air mass flow rate is \( 25 \mathrm{~kg} / \mathrm{s} \). The compressor pressure ratio is 9 , the turbine inlet temperature is \( 1400 \mathrm{~K} \), and air exits the nozzle at \( 26 \mathrm{kPa} \). The diffuser and nozzle processes are isentropic, the compressor and turbine have isentropic efficiencies of \( 85 \% \) and \( 90 \% \), respectively, and there is no pressure drop for flow through the combustor. Kinetic energy is negligible everywhere except at the diffuser inlet and the nozzle exit. The states are numbered as in the figure below. On the basis of air-standard analysis, determine: (a) the pressures, in \( \mathrm{KPa} \), and temperatures, in \( \mathrm{K} \), at each principal state. (b) the rate of heat addition to the air passing through the combustor, in \( \mathrm{kJ} / \mathrm{s} \). (c) the velocity at the nozzle exit, in \( \mathrm{m} / \mathrm{s} \).