(Solved): A study was done using a treatment group and a placebo group. The results are shown in the table As ...

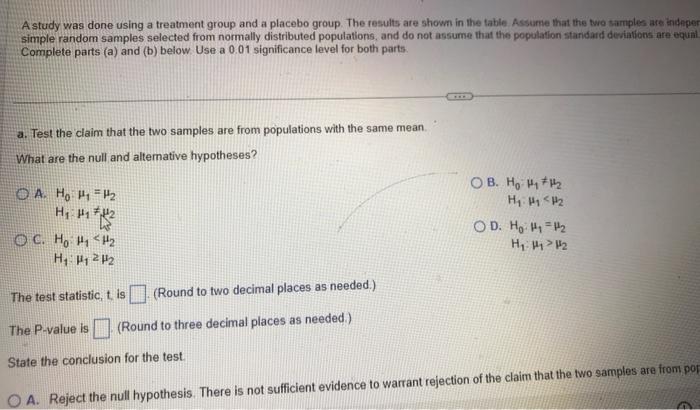
A study was done using a treatment group and a placebo group. The results are shown in the table Assurne that the two tamples are thiteper simple random samples selected from normally distributed populations, and do not assume that the population stanidard deriations are equal Complete parts (a) and (b) below. Use a \( 0.01 \) significance level for both parts a. Test the claim that the two samples are from populations with the same mean What are the null and altemative hypotheses? A. \( \mathrm{H}_{0}: \mu_{1}=\mu_{2} \) B. \( H_{0} \cdot \mu_{1} \neq \mu_{2} \) \( H_{1}: \mu_{1} \neq \mu_{2} \) D. \( H_{0} \cdot \mu_{1}=\mu_{2} \) C. \( H_{0}: \mu_{1}<\mu_{2} \) \( H_{1}: \mu_{1}>\mu_{2} \) \( H_{1}: \mu_{1}: \mu_{2} \) The test statistic, \( t \), is (Round to two decimal places as needed.) The P-value is (Round to three decimal places as needed) State the conclusion for the test. A. Reject the null hypothesis. There is not suificient evidence to warrant rejection of the claim that the two samples are from pof e shown in the table. Assume that the two samples are independent not assume that the population standard deviations are equal. B. \( H_{0}: \mu_{1} \neq \mu_{2} \) \( H_{1}: \mu_{1}<\mu_{2} \) D. 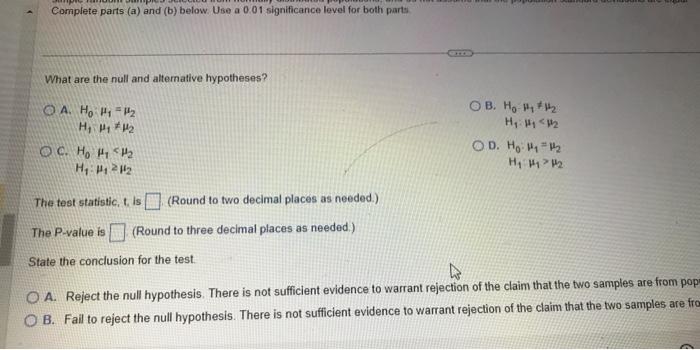\( H_{0}: \mu_{1}=\mu_{2} \) \( H_{1}: \mu_{1}>\mu_{2} \) What are the null and alternative hypotheses? A. \( H_{0}: \mu_{1}=\mu_{2} \) B. \( H_{0}-\mu_{1}+\mu_{2} \) \( H_{1}, \mu_{1} \neq \mu_{2} \) \( H_{1}: \mu_{1}<\mu_{2} \) c. \( H_{0} \quad \mu_{1}<\mu_{2} \) D. \( H_{0} \cdot \mu_{1}=\mu_{2} \) \( H_{1}: \mu_{1} \geq \mu_{2} \) \( H_{1} \mu_{1}>\mu_{2} \) The test statistic, t. Is (Round to two decimal places as needed.) The P-value is (Round to three decimal places as needed.) State the conclusion for the test. A. Reject the null hypothesis. There is not sufficient evidence to warrant rejection of the claim that the two samples are from pop B. Fail to reject the null hypothesis. 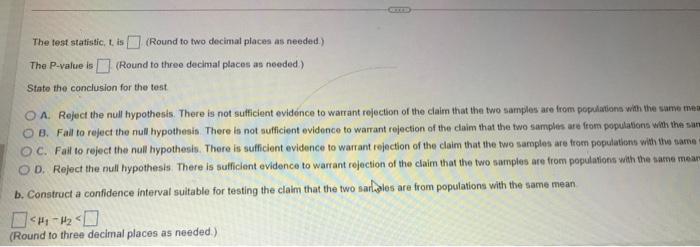There is not sufficient evidence to warrant rejection of the claim that the two samples are fro The test statistic, 1, is (Round to two decimal places as needed) The P-value is (Round to three decimal places as needed) State the conclusion for the test. A. Reject the null hypothesis. There is not sufficient evidence to warrant rejection of the ciairn that the two samples are from populations with the same tiet B. Fail to reject the null hypothesis. There is not sufficient evidence to warrant rejection of the claim that the two samplies are from populations with then sar C. Fail to reject the null hypothesis. There is sufficient evidence to warrant rejection of the claim that the two sarnples are trom populatisns with the tarne D. Reject the null hypothesis. There is sufficient evidence to warrant rejection of the claim that the two samples are from populations with the iasne mear b. Construct a confidence interval suitable for testing the claim that the two sarfales are from populations with the same mean \[ <\mu_{1}-\mu_{2}< \] (Round to three decimal places as needed.)