(Solved): A Student cycle engine is analyzed using the cold air-standard method. Given the definition of each ...

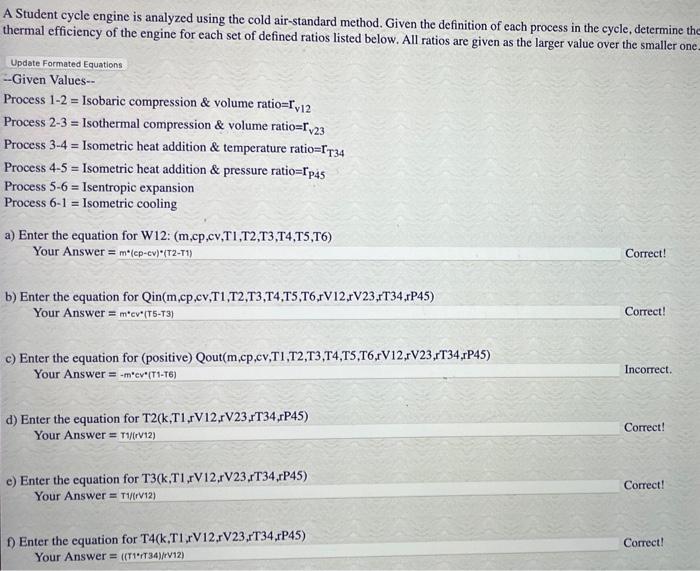
A Student cycle engine is analyzed using the cold air-standard method. Given the definition of each process in the cycle, determine the thermal efficiency of the engine for each set of defined ratios listed below. All ratios are given as the larger value over the smaller one Update Formated Equations -Given Values-. Process \( 1-2 \) = Isobaric compression \& volume ratio= \( \mathrm{r}_{\mathrm{v} 12} \) Process 2-3 = Isothermal compression \& volume ratio \( =\mathrm{r}_{\sqrt{23}} \) Process \( 3-4= \) Isometric heat addition \& temperature ratio= \( \mathrm{r}_{\mathrm{T} 34} \) Process 4-5 \( = \) Isometric heat addition \& pressure ratio \( =\mathrm{r}_{\mathrm{P}} 45 \) Process 5-6 = Isentropic expansion Process 6-1 = Isometric cooling a) Enter the equation for W12: (m,cp,cv,T1,T2,T3,T4,T5,T6) Your Answer \( =m^{*}(e p-e v) *(T 2-T 1) \) Correct! b) Enter the equation for Qin(m,cp,cv,T1,T2,T3,T4,T5,T6,rV12,rV23,rT34,rP45) Your Answer \( =m^{*} \operatorname{cr}^{*}(T 5-T 3) \) Correct! c) Enter the equation for (positive) Qout(m,cp,cv,T1,T2,T3,T4,T5,T6,rV12,rV23,rT34,rP45) Your Answer \( =-m^{*} \operatorname{cr}^{\circ}( \) (T1-T6) Incorrect. d) Enter the equation for T2(k,T1,rV12,rV23,rT34,rP45) Your Answer \( =\mathrm{T} /(\mathrm{r} \mathbf{1} 12) \) Correct! e) Enter the equation for T3(k,T1,rV12,rV23,rT34,rP45) Your Answer \( = \) T1/(r 12) Correct! f) Enter the equation for T4(k,T1,rV12,rV23,rT34,rP45) Your Answer \( =((\tau 1 \cdot \tau 34))(r \) 12) \( ) \) Correct! 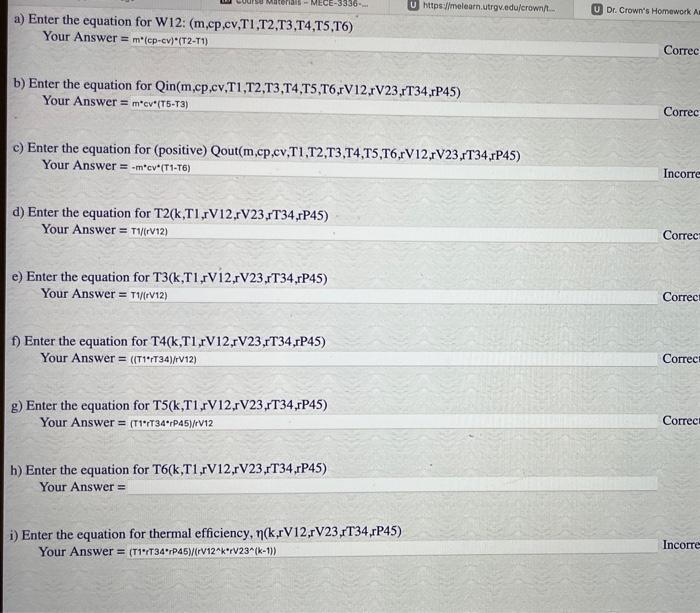a) Enter the equation for W12: (m,cp,cv,T1,T2,T3,T4,T5,T6) Your Answer \( =m^{*} \cdot( \) (ep-cev) \( \cdot(T 2-T)) \) b) Enter the equation for \( \mathrm{Qin}(\mathrm{m}, \mathrm{cp}, \mathrm{cc}, \mathrm{T} 1, \mathrm{~T} 2, \mathrm{~T} 3, \mathrm{~T} 4, \mathrm{~T} 5, \mathrm{~T} 6, \mathrm{rV} 12, \mathrm{rV} 23, \mathrm{rT} 34, \mathrm{rP} 45) \) Your Answer \( =m^{*} \) cev (T5-T3) c) Enter the equation for (positive) Qout(m,cp,cv,T1,T2,T3,T4,T5,T6,rV12,rV23,rT34,rP45) Your Answer \( =-^{*} \cdot \operatorname{cv}^{*} \cdot(T 1-T 6) \) d) Enter the equation for T2(k,T1,rV12,rV23,rT34,rP45) Your Answer \( =T \) T1/(rV12) e) \( \mathrm{Er} \) f) \( \mathrm{Er} \) g) Enter the equation for T5(k,T1,rV12,rV23,rT34,rP45) h) Enter the equation for T6(k,T1,rV12,rV23,rT34,rP45) Your Answer \( = \) i) Enter the equation for thermal efficiency, \( \eta(\mathrm{k}, \mathrm{rV} 12, \mathrm{rV} 23, \mathrm{~T} 34, \mathrm{rP} 45) \) Your Answer \( =\left(\pi \oplus \cdot T 34^{*} \cdot p 45\right)\left(\left(r v 12^{\wedge} k^{*} \cdot v 23^{\wedge}(k-1)\right)\right. \)