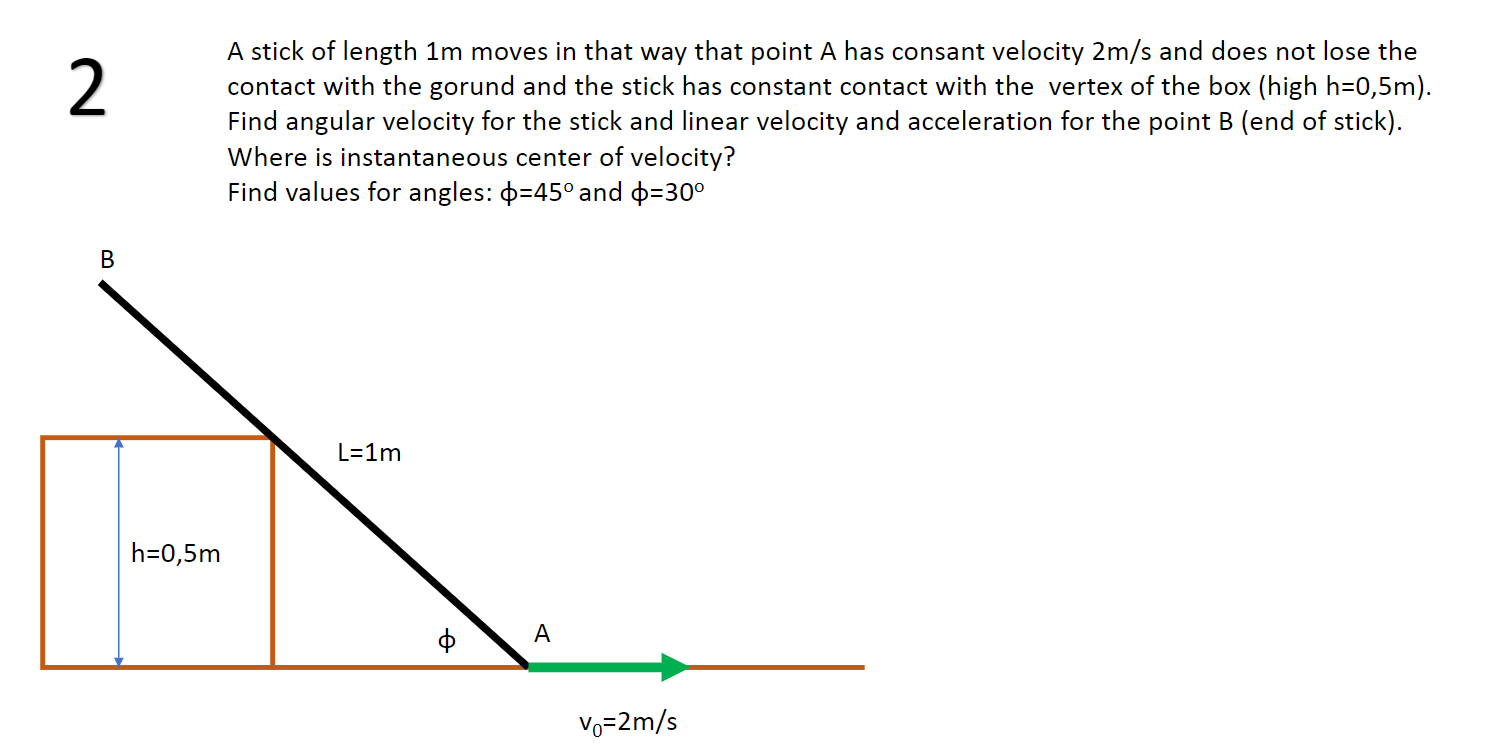
(Solved): A stick of length \( 1 \mathrm{~m} \) moves in that way that point \( A \) has consant velocity \( ...

A stick of length \( 1 \mathrm{~m} \) moves in that way that point \( A \) has consant velocity \( 2 \mathrm{~m} / \mathrm{s} \) and does not lose the contact with the gorund and the stick has constant contact with the vertex of the box (high \( \mathrm{h}=0,5 \mathrm{~m}) \). Find angular velocity for the stick and linear velocity and acceleration for the point B (end of stick). Where is instantaneous center of velocity? Find values for angles: \( \phi=45^{\circ} \) and \( \phi=30^{\circ} \)