(Solved): A solid cylinder of mass M and uniform density is rolling, without slipping, down a plane inclined a ...
A solid cylinder of mass M and uniform density is rolling, without slipping, down a plane inclined at an angle ? to the horizontal, as shown in the diagram below, where we have depicted the cylinder at time t = 0 and some later time t > 0. Please note very carefully the notation introduced in this diagram. The axis of the cylinder points out of the page.
The forces acting on the cylinder are a normal reaction force R, friction force Ffric, and the weight force. It is clear that we can write
Ffric = F I, R = R J,
where F, R are scalars and I, J are the orthogonal unit vectors along and normal to the
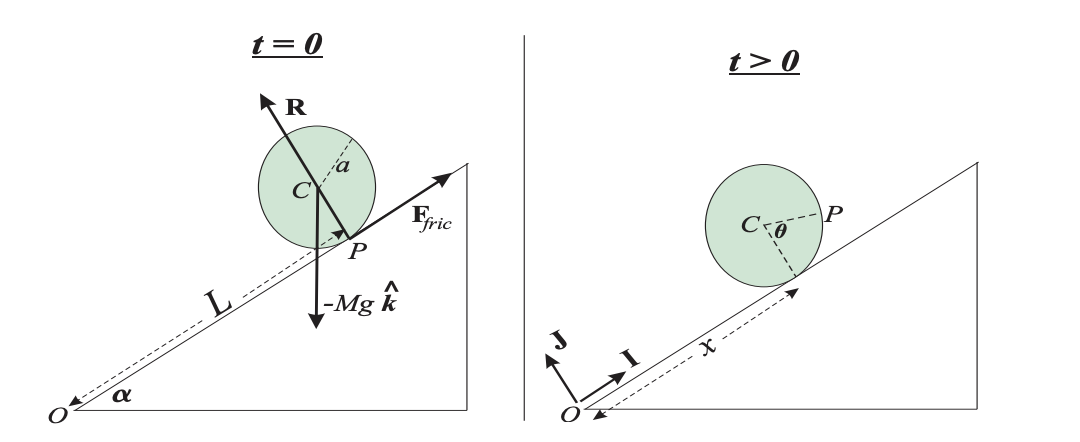
(b) By considering the total external torque about the centre of mass C of the cylinder, show that: d^2?/dt2 = 2F /M a.
(c) Show that the rolling condition implies that: L - x = a?, and use this condition, together with your results from Parts (a) and (b), to find the acceleration of the centre of mass of the cylinder.
(d) Calculate the total mechanical energy (kinetic plus potential) of the cylinder during the motion. Show that this energy is conserved during the motion.
Important info
