(Solved): A parallel plate capacitor has capacitance \( C_{0} \), plate separation \( d \) and plate area \( ...

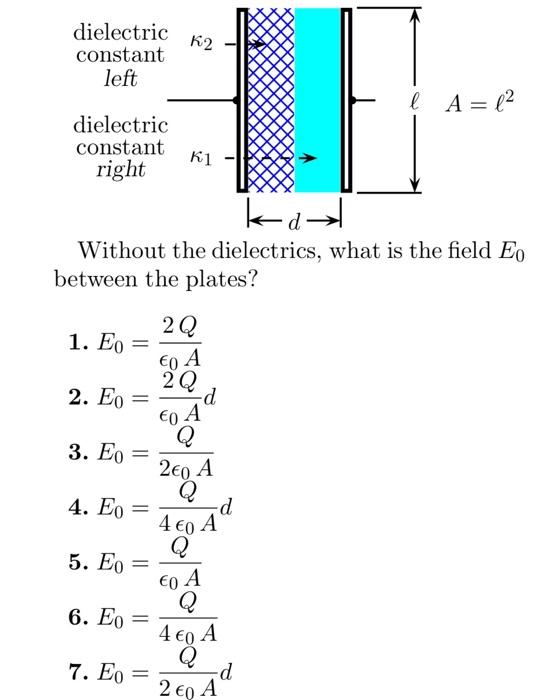
A parallel plate capacitor has capacitance \( C_{0} \), plate separation \( d \) and plate area \( A \). Two dielectric slabs of dielectric constants \( \kappa_{1} \) and \( \kappa_{2} \), each of thickness \( \frac{d}{2} \), are inserted between the plates. Charges \( Q \) and \( -Q \) are put on the upper and lower plates. Without the dielectrics, what is the field \( E_{0} \) between the plates? 1. \( E_{0}=\frac{2 Q}{\epsilon_{0} A} \) 2. \( E_{0}=\frac{2 Q}{\epsilon_{0} A} d \) 3. \( E_{0}=\frac{Q}{2 \epsilon_{0} A} \) 4. \( E_{0}=\frac{Q}{4 \epsilon_{0} A} d \) 5. \( E_{0}=\frac{Q}{\epsilon_{0} A} \) 6. \( E_{0}=\frac{Q}{4 \epsilon_{0} A} \) 7. \( E_{0}=\frac{Q}{2 \epsilon_{0} A} d \) With the dielectrics inserted, the fields in \( \kappa_{1} \) and \( \kappa_{2} \) are respectively 1. \( E_{1}=\frac{E_{0}}{\kappa_{1}} \) and \( E_{2}=\frac{E_{0}}{\kappa_{2}} \) 2. \( E_{1}=E_{0} \kappa_{2} \) and \( E_{2}=E_{0} \kappa_{1} \) 3. \( E_{1}=E_{0} \kappa_{1} \) and \( E_{2}=E_{0} \kappa_{2} \) 4. \( E_{1}=\frac{E_{0}}{\kappa_{2}} \) and \( E_{2}=\frac{E_{0}}{\kappa_{1}} \) 5. \( E_{1}=\frac{E_{0} \kappa_{1}}{\kappa_{1}+\kappa_{2}} \) and \( E_{2}=\frac{E_{0} \kappa_{2}}{\kappa_{1}+\kappa_{2}} \) 6. \( E_{1}=\frac{E_{0} \kappa_{2}}{\kappa_{1}+\kappa_{2}} \) and \( E_{2}=\frac{E_{0} \kappa_{1}}{\kappa_{1}+\kappa_{2}} \) 7. \( E_{1}=\frac{E_{0} \kappa_{1} \kappa_{2}}{\kappa_{1}+\kappa_{2}} \) and \( E_{2}=\frac{E_{0} \kappa_{1} \kappa_{2}}{\kappa_{1}+\kappa_{2}} \) 010 (part 3 of 3 ) \( 10.0 \) points Let \( \kappa_{1}=2.9, \kappa_{2}=3.2, A=1.05 \mathrm{~m}^{2} \), and \( d=0.46 \mathrm{~mm} \). What is the resultant capacitance? Answer in units of \( \mathrm{F} \).