(Solved): A free-body diagram is a useful tool when using Newton's second law to solve physics problems. How ...

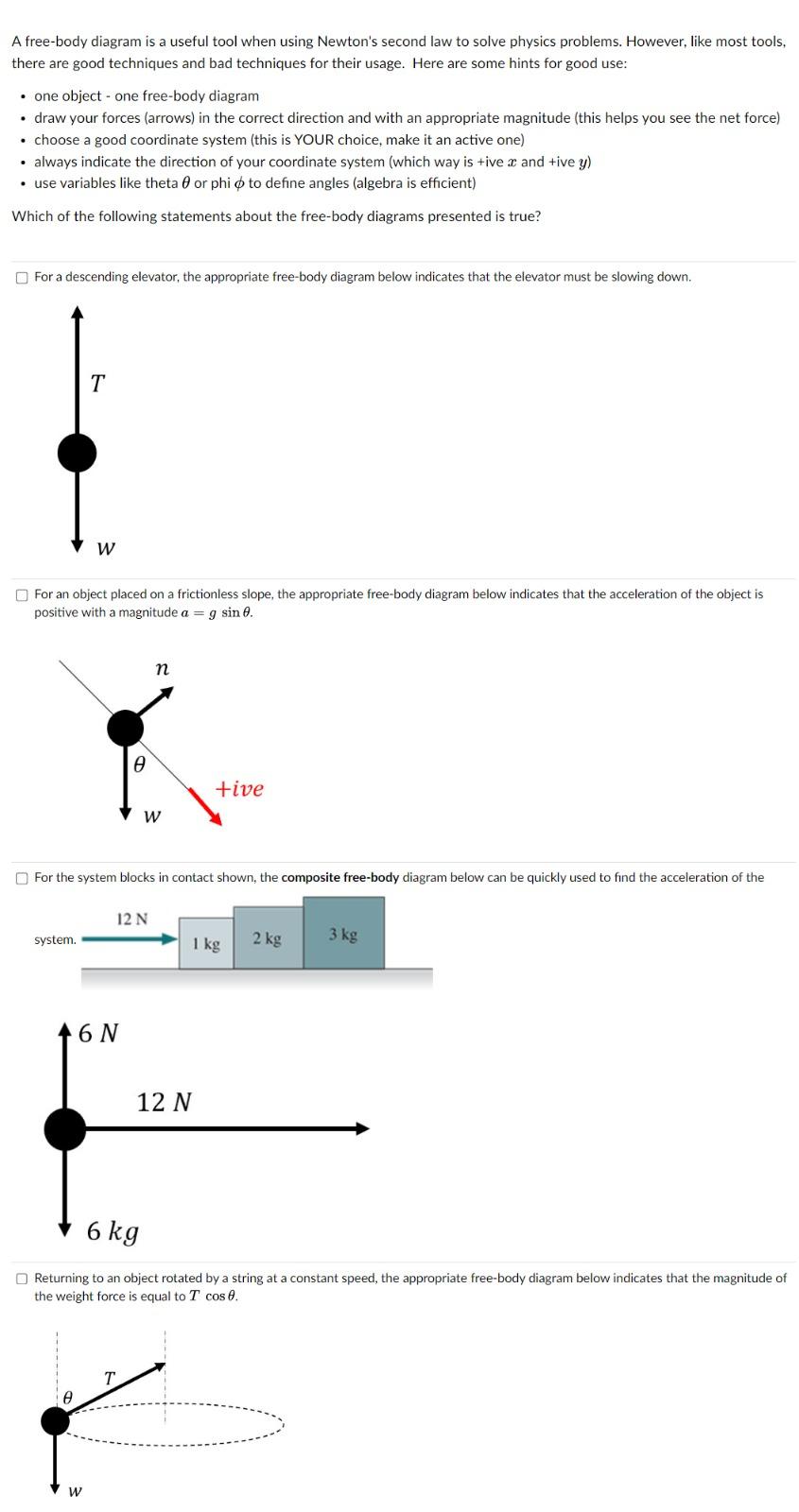
A free-body diagram is a useful tool when using Newton's second law to solve physics problems. However, like most tools, there are good techniques and bad techniques for their usage. Here are some hints for good use: - one object - one free-body diagram - draw your forces (arrows) in the correct direction and with an appropriate magnitude (this helps you see the net force) - choose a good coordinate system (this is YOUR choice, make it an active one) - always indicate the direction of your coordinate system (which way is +ive \( x \) and +ive \( y \) ) - use variables like theta \( \theta \) or phi \( \phi \) to define angles (algebra is efficient) Which of the following statements about the free-body diagrams presented is true? For a descending elevator, the appropriate free-body diagram below indicates that the elevator must be slowing down. For an object placed on a frictionless slope, the appropriate free-body diagram below indicates that the acceleration of the object positive with a magnitude \( a=g \sin \theta \). For the system blocks in contact shown, the composite free-body diagram below can be quickly used to find the acceleration of the Returning to an object rotated by a string at a constant speed, the appropriate free-body diagram below indicates that the magnitude of the weight force is equal to \( T \cos \theta \). Friction acts in almost all situations. We have been ignoring friction to develop an understanding of Newton's laws but wil now include this in our understanding of motion. Friction is modelled as a constant force that opposes the relative motion of two surfaces. Importantly it has two manifestations. For situations where the surfaces do not move relative to each other \( F_{\text {static }} \leq-\mu_{s} n \). For situations where the surfaces do move relative to each other \( F_{k i n e t i c}=-\mu_{k} n \) Which of the following statements about friction are true? Consider an object that slides down a slope with friction (correct free-body diagram below). The magnitude of the force of friction must be equal to \( \mu_{s} m g \cos \theta \) The coefficient of static friction is greater than the coefficient of kinetic friction for two surfaces in contact. Consider a wheel that is rolling along a horizontal road with friction. The force of friction that acts on the wheel is the kinetic force of friction as the wheel is in motion. For an object that just starts to slide down a slope that is inclined at 45 degrees, the coefficient of kinetic friction is \( 1 . \) Consider a box on a horizontal surface with friction. If you slowly increase the force you apply the box will remain stationary until the force you apply is equal in magnitude to \( \mu_{k} m g \), at which point the box will accelerate.