Home /
Expert Answers /
Other Math /
a-fence-30-feet-tall-runs-parallel-to-a-tall-building-at-a-distance-of-6-ft-from-the-building-as-sho-pa402
(Solved): A fence 30 feet tall runs parallel to a tall building at a distance of 6 ft from the building as sho ...
A fence 30 feet tall runs parallel to a tall building at a distance of 6 ft from the building as shown in the diagram. ? LADDER 1 6 ft. feet 30 ft We wish to find the length of the shortest ladder that will reach from the ground over the fence to the wall of the building. [A] First, find a formula for the length of the ladder in terms of 0. (Hint: split the ladder into 2 parts.) Type theta for 0. I L(0) [B] Now, find the derivative, L'(0). Type theta for 0. L'(0) [C] Once you find the value of that makes L'(0) = 0, substitute that into your original function to find places.) the length of the shortest ladder. (Give your answer accurate to 5 decim L(0min)~
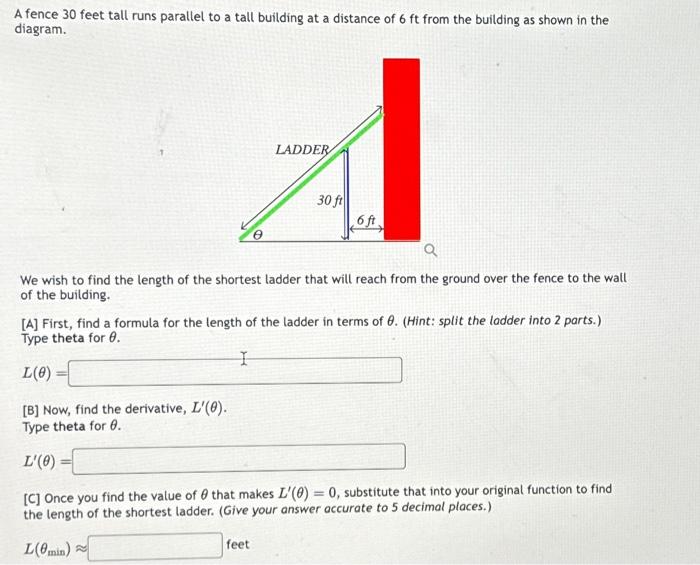
A fence 30 feet tall runs parallel to a tall building at a distance of from the building as shown in the diagram. We wish to find the length of the shortest ladder that will reach from the ground over the fence to the wall of the building. [A] First, find a formula for the length of the ladder in terms of . (Hint: split the ladder into 2 parts.) Type theta for . [B] Now, find the derivative, . Type theta for . [C] Once you find the value of that makes , substitute that into your original function to find the length of the shortest ladder. (Give your answer accurate to 5 decimal places.)
Expert Answer
To find the shortest length of ladder leaning from a tall building over the fence of height 30 feet, 6 feet away from the building (a) We need to find length of ladder as (length in terms of theta) (b) To find minimum value of we need to find (c) After finding minimum theta we can find into feet upto 5 decimal places.