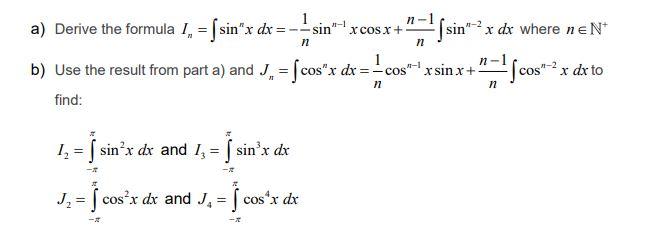(Solved): a) Derive the formula \( I_{n}=\int \sin ^{n} x d x=-\frac{1}{n} \sin ^{n-1} x \cos x+\frac{n-1}{n ...

a) Derive the formula \( I_{n}=\int \sin ^{n} x d x=-\frac{1}{n} \sin ^{n-1} x \cos x+\frac{n-1}{n} \int \sin ^{n-2} x d x \) where \( n \in \mathbb{N}^{+} \) b) Use the result from part a) and \( J_{n}=\int \cos ^{n} x d x=\frac{1}{n} \cos ^{n-1} x \sin x+\frac{n-1}{n} \int \cos ^{n-2} x d x \) to find: \[ \begin{array}{l} I_{2}=\int_{-\pi}^{\pi} \sin ^{2} x d x \text { and } I_{3}=\int_{-\pi}^{\pi} \sin ^{3} x d x \\ J_{2}=\int_{-\pi}^{\pi} \cos ^{2} x d x \text { and } J_{4}=\int_{-\pi}^{\pi} \cos ^{4} x d x \end{array} \]