(Solved): a) Derive the following expression using the definitions of the common-emitter current gain \( \be ...

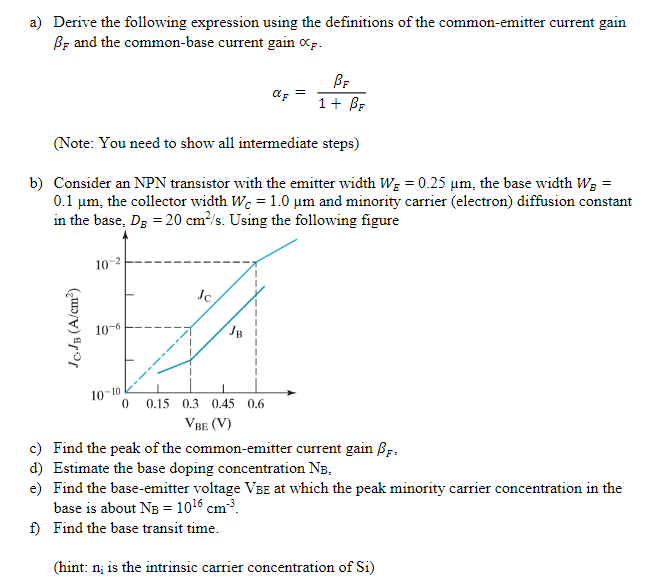
a) Derive the following expression using the definitions of the common-emitter current gain \( \beta_{F} \) and the common-base current gain \( \propto_{F} \). \[ \alpha_{F}=\frac{\beta_{F}}{1+\beta_{F}} \] (Note: You need to show all intermediate steps) b) Consider an NPN transistor with the emitter width \( W_{E}=0.25 \mu \mathrm{m} \), the base width \( W_{B}= \) \( 0.1 \mu \mathrm{m} \), the collector width \( W_{C}=1.0 \mu \mathrm{m} \) and minority carrier (electron) diffusion constant in the base, \( D_{B}=20 \mathrm{~cm}^{2} / \mathrm{s} \). Using the following figure c) Find the peak of the common-emitter current gain \( \beta_{F} \); d) Estimate the base doping concentration \( \mathrm{N}_{\mathrm{B}} \), e) Find the base-emitter voltage \( V_{B E} \) at which the peak minority carrier concentration in the base is about \( \mathrm{N}_{\mathrm{B}}=10^{16} \mathrm{~cm}^{-3} \). f) Find the base transit time. (hint: \( \mathrm{n}_{\mathrm{i}} \) is the intrinsic carrier concentration of \( \mathrm{Si} \) )