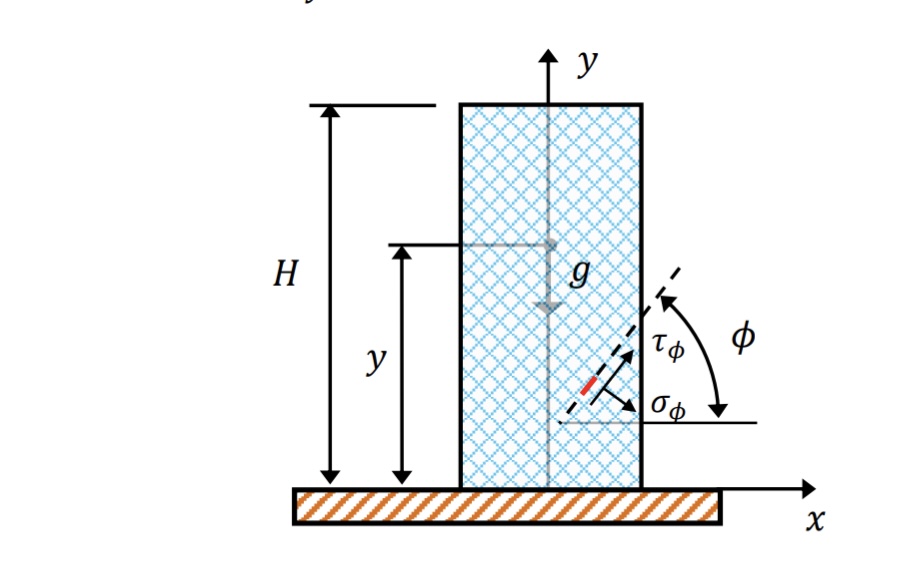
(Solved): A concrete column of mass density supports its own weight, as shown in the figure below. (Assum ...

A concrete column of mass density ???? supports its own weight, as shown in the figure below. (Assume that the
solid is subjected to a uniform gravitational body force of magnitude ???? per unit mass).
a) Show that the stress distribution ???????? = ?????????(???? ? ????) and ???????? = ???????????? = 0 satisfies the two-dimensional stress
equilibrium equations.
[10 marks]
b) Suppose that the concrete contains a large number of randomly oriented micro-cracks. A crack which lies at
an angle ???? to the ????-axis will propagate if
(????????)2
+ ???????????? ? ????0
where ???????? and ???????? are normal and shear stress acting on the plane defined by angle ????, ???? is the friction coefficient
between faces of the crack and ????0 is a critical shear stress that is related to the size of the micro-cracks and the
fracture toughness of the concrete, and is therefore a material property (we will talk about fracture properties in
Lecture 6).
Assume that ???? = 0.5. Find the orientation of the micro-crack that is most likely to propagate.
[20 marks]
c) For the same friction coefficient as in b) (???? = 0.5) find an expression for the maximum possible height of the
column as a function of its material properties and free acceleration, ????. Obtain the value of the maximum possible
height of concrete columns (without reinforcement) if ???? = 3000 kg m-3
, ????0 = 50 MPa and ???? = 9.8 m s
-2
.???????