(Solved): A concerned group of citizens wanted to know if the proportion of armed robberies in Texas was diff ...

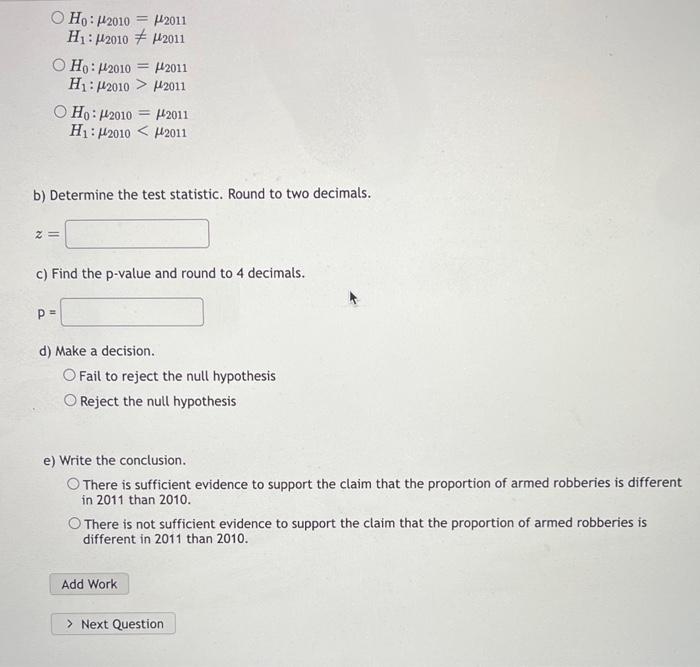
A concerned group of citizens wanted to know if the proportion of armed robberies in Texas was different in 2011 than in 2010. Their research showed that of the 113,231 violent crimes in Texas in 2010, 7,622 of them were armed robberies. In \( 2011,7,439 \) of the 104,873 violent crimes were in the armed robbery category. Test at a \( 5 \% \) significance level. a) The null and alternative hypothesis would be: \( H_{0}: p_{2010}=p_{2011} \) \( H_{1}: p_{2010}p_{2011} \) \( H_{0}: \mu_{2010}=\mu_{2011} \) \( H_{1}: \mu_{2010} \neq \mu_{2011} \) \( H_{0}: \mu_{2010}=\mu_{2011} \) \( H_{1}: \mu_{2010}>\mu_{2011} \) \( H_{0}: \mu_{2010}=\mu_{2011} \) \( H_{1}: \mu_{2010}<\mu_{2011} \) b) Determine the test statistic. Round to two decimals. \( z= \) c) Find the \( p \)-value and round to 4 decimals. \[ p= \] d) Make a decision. Fail to reject the null hypothesis Reject the null hypothesis \[ \begin{array}{l} H_{0}: \mu_{2010}=\mu_{2011} \\ H_{1}: \mu_{2010} \neq \mu_{2011} \\ H_{0}: \mu_{2010}=\mu_{2011} \\ H_{1}: \mu_{2010}>\mu_{2011} \\ H_{0}: \mu_{2010}=\mu_{2011} \\ H_{1}: \mu_{2010}<\mu_{2011} \end{array} \] b) Determine the test statistic. Round to two decimals. \[ z= \] c) Find the \( \mathrm{p} \)-value and round to 4 decimals. \[ p= \] d) Make a decision. Fail to reject the null hypothesis Reject the null hypothesis e) Write the conclusion. There is sufficient evidence to support the claim that the proportion of armed robberies is different in 2011 than 2010. There is not sufficient evidence to support the claim that the proportion of armed robberies is different in 2011 than 2010.