(Solved): A. Complete the table below by entering the missing name or atomic symbol. B. Complete the table be ...

A. Complete the table below by entering the missing name or atomic symbol. B. Complete the table below by entering the missing isotope name or symbol. C. Which has more neutrons? Show your work in the box below. D. ReDort the atomic masses of the following elements to two decimal places. E. Complete the table below. F. An early version of the Periodic Table had the elements listed in order of increasing relative atomic mass instead of increasing atomic number. Doing so today would result in the reordering of three pairs of elements in the first 5 periods. For example: argon has a larger mass than potassium, making \( \mathrm{Ar} \) and \( \mathrm{K} \) one of the pairs. Identify the other two element-pairs. G. Write the symbol of the element on the right which matches its description on the left. - a dark red liquid element found in period 4 \( \begin{array}{ll} & \mathrm{Pb} \\ & \mathrm{Ca} \\ \mathrm{BA} & \mathrm{Br} \\ & \mathrm{C}\end{array} \) H. Match the element on the left with its classification on the right. You may use each classification more than once, or not at all. A. noble gas radium B. transition element rubidium C. alkali metal plutonium D. alkaline earth metal sine E. actinoid F. 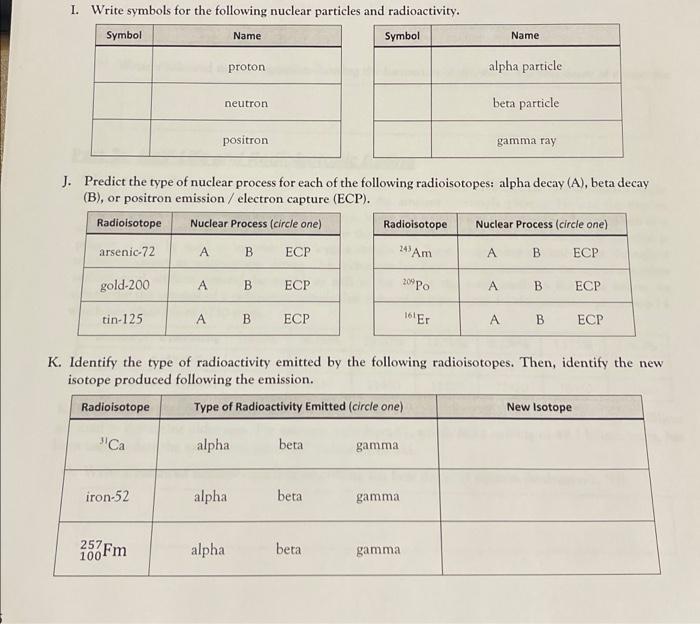halogen I. Write symbols for the following nuclear particles and radioactivity. J. Predict the type of nuclear process for each of the following radioisotopes: alpha decay (A), beta decay (B), or positron emission / electron capture (ECP). K. Identify the type of radioactivity emitted by the following radioisotopes. Then, identify the new isotope produced following the emission. L. Balance the following nuclear equations by writing the symbol of the missing particle in each box. \[ { }_{52} 21 \mathrm{Te} \rightarrow{ }_{51}^{121} \mathrm{Sb}+ \] \[ \underset{27}{60} \mathrm{Co} \rightarrow{ }_{28}^{60} \mathrm{Ni}+ \] M. Polonium-213 undergoes alpha decay to produce a radioisotope. That daughter radioisotope undergoes beta decay to produce a stable granddaughrer isotope. Identify the stable granddaughter isorope. N. Write a balanced nuclear equation showing the formation of zinc-66 by the beta decay of copper-66. Part 3: Half-Life and Radioisotopic Dating While studying the properties of radioactivity, Ernest Rutherford discovered that the rate at which a single isotope undergoes nuclear decay is independent of the amount of sample present. He was the first to measure the half-life associated with a radioisotope, where the half-life is the time required for one-half of a sample of radioactive material to decay. Because the halffife does not depend on how much material is present, it can be used to measure how long a sample has been undergoing nuclear decay through a technique known as radioisotopic dating. This technique has been used to derermine the age of countless archeological artifacts around the world, as well as the age of the earth itself. In the table below, we summarize the amount of a radioactive sample that remains as time passes for the radioisotope carbon-14. which has a half-life of 5730 years. Radiocarbon dating can be used to date objects up to 60,000 years old. Other isotopes with longer halt-lives are used to determine older ages. For example, rubidium 87 , which has a half-life of \( 49.2 \) billion years, has been used to date the earth to an age of \( 4.5 \) million years old. O Write a balanced nuclear equation describing the beta decay of tritium (hydrogen-3, \( \left.{ }^{3} \mathrm{H}\right) \). 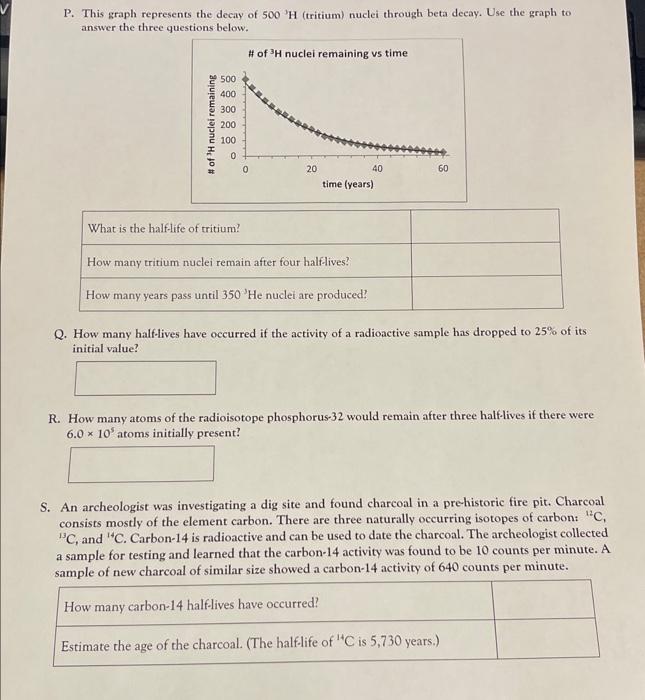P. This graph represents the decay of \( 500^{-} \mathrm{H} \) (tritium) nuclei through beta decay. Use the graph to answer the three questions below. Q. How many half-lives have occurred if the activity of a radioactive 5 ample has dropped to \( 25 \% \) of its initial value? R. How many atoms of the radioisotope phosphorus-32 would remain after three half-lives if there were \( 6.0 \times 10^{5} \) atoms initially present? S. An archeologist was investigating a dig site and found charcoal in a prehistoric fire pit. Charcoal consists mostly of the element carbon. There are three naturally occurring isotopes of carbon: \( { }^{12} \mathrm{C} \), \( { }^{13} \mathrm{C} \), and \( { }^{14} \mathrm{C} \). Carbon-14 is radioactive and can be used to date the charcoal. The archeologist collected a sample for testing and learned that the carbon-14 activity was found to be 10 counts per minute. A sample of new charcoal of similar size showed a carbon-14 activity of 640 counts per minute.