(Solved): A coil is suspended around an axis which is co-linear with the axis of a bar magnet. The coil is ...

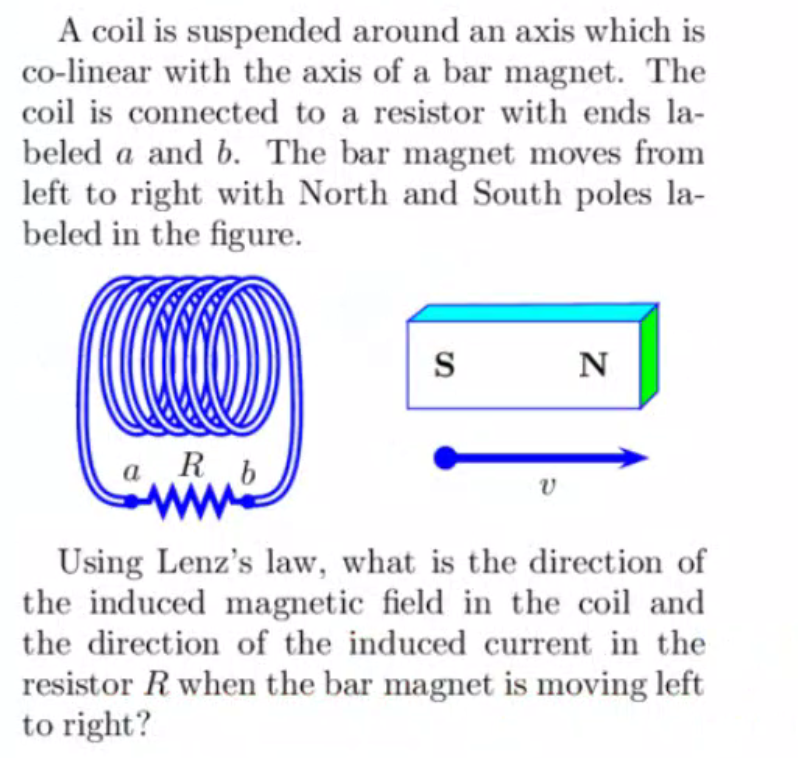
A coil is suspended around an axis which is co-linear with the axis of a bar magnet. The coil is connected to a resistor with ends labeled \( a \) and \( b \). The bar magnet moves from left to right with North and South poles labeled in the figure. \( v \) Using Lenz's law, what is the direction of the induced magnetic field in the coil and the direction of the induced current in the resistor \( R \) when the bar magnet is moving left to right? The induced magnetic field is right to left 1. \( \left(\Longleftarrow B_{\text {induced }}\right) \) and the induced current flows from \( a \) through \( R \) to \( b(I \longrightarrow) \). The induced magnetic field is zero and the 2. induced current flows from \( a \) through \( R \) to \( b \) \( (I \longrightarrow) \) The induced magnetic field is left to right 3. ( \( B_{\text {induced }} \Longrightarrow \) ) and the induced current flows from \( a \) through \( R \) to \( b(I \longrightarrow) \). The induced magnetic field is zero and the 4. induced current flows from \( b \) through \( R \) to \( a \) \( (\longleftarrow I) \) The induced magnetic field is right to left \( \left(\Longleftarrow B_{\text {induced }}\right) \) and the induced current is zero. The induced magnetic field is zero and the induced current is zero. The induced magnetic field is left to right \( \left(B_{\text {induced }} \Longrightarrow\right) \) and the induced current is zero. The induced magnetic field is right to left 8. \( \left(\Longleftarrow B_{\text {induced }}\right) \) and the induced current flows from \( b \) through \( R \) to \( a(\longleftarrow I) \). The induced magnetic field is left to right 9. \( \left(B_{\text {induced }} \Longrightarrow\right. \) ) and the induced current flows from \( b \) through \( R \) to \( a(\longleftarrow I) \).