(Solved): A 4 noded quadrilateral element is shown below The \( (x, y) \) coordinates (in \( \mathrm{mm} \ ...

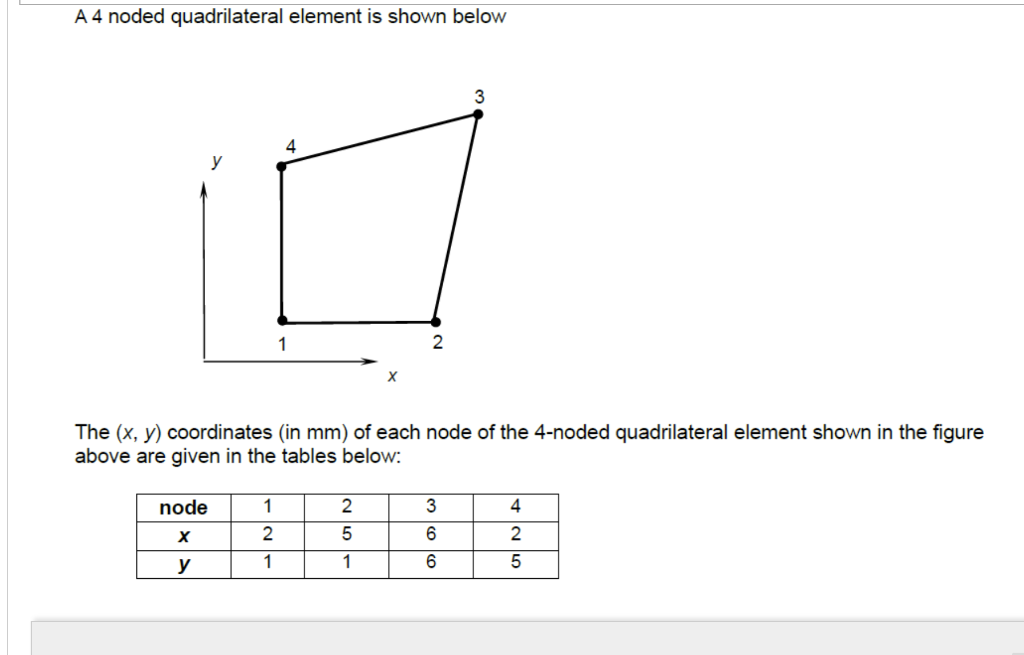
A 4 noded quadrilateral element is shown below The \( (x, y) \) coordinates (in \( \mathrm{mm} \) ) of each node of the 4-noded quadrilateral element shown in the figure above are given in the tables below: 1) Determine the Jacobian matrix \( [\mathrm{J}] \) and \( [\mathrm{J}]^{-1} \) for the element. ( 20 marks) 2) Evaluate the integral below using \( 2 \times 2 \) Gauss-Legendre quadrature: (5 marks) \[ I=\iint_{A}(x+y) d x d y \] where \( \mathrm{A} \) denotes the region shown in figure above. Note: Change of variables formula (from \( x, y \) coordinates to \( \xi, \eta \) coordinates) for double integrals is given by \[ \iint_{A} f(x, y) d x d y=\int_{-1}^{1} \int_{-1}^{1} f(x(\xi, \eta), y(\xi, \eta))|J| d \xi d \eta \] where \( \mid \mathrm{JI} \) is the determinant of the Jacobian matrix [ \( \mathrm{J}] \).