(Solved): 6. The binomial test and its relationship to the chi-square test Does advertising influence childr ...

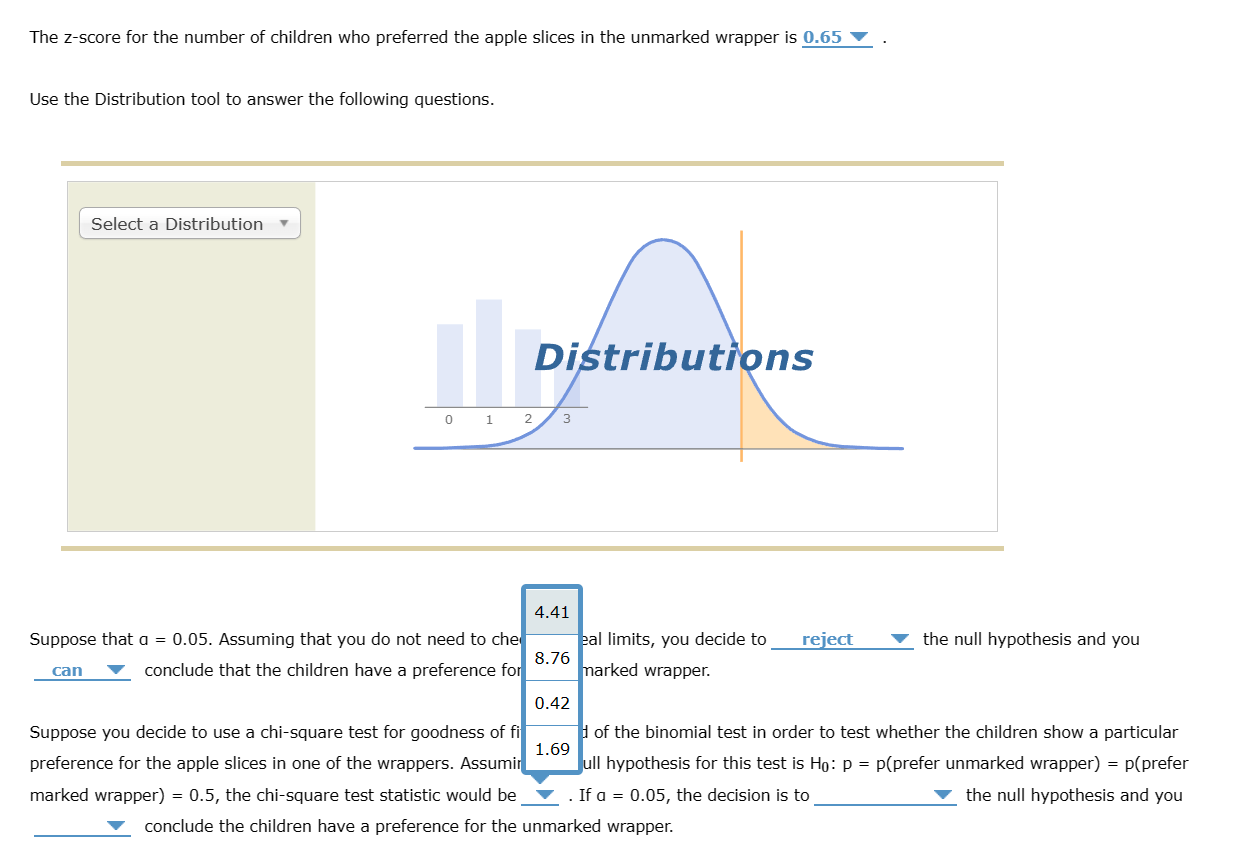
6. The binomial test and its relationship to the chi-square test Does advertising influence children as young as three? Researchers at Stanford University conducted a taste test with preschoolers. Each preschooler tasted two identical samples of five food items (hamburger, french fries, chicken nuggets, baby carrots, and milk). For each item, the children tasted one sample wrapped in a McDonald's wrapper and the other sample in an identical, but unbranded, wrapper. Some children tasted the sample in the branded wrapper first, others tasted the sample in the unbranded wrapper first. Consistently for all food items, the majority of preschoolers preferred the food in the McDonald's wrapper over the one in the unbranded wrapper, even though both samples were identical. (Source: Robinson, T. N., et al. "Effects of fast food branding on young children's taste preferences." Archives of Pediatrics \& Adolescent Medicine 161 [2007]: 792-797) The researchers found that the preschoolers who watched more television or ate more often at McDonald's were more likely to prefer the food wrapped in a McDonald's wrapper. However, is it possible that the children were attracted to the branded wrapper because it had more writing and colors on it, rather than because they recognized the McDonald's logo? You decide to conduct a similar experiment among 83 preschoolers using identical samples of apple slices. In this experiment, you wrap one of the identical samples in a wrapper that is colorfully marked and lettered with a description of the contents and the other in an unmarked, unlabeled wrapper of the same size, shape, and material. In your experiment, 55 of the 83 children preferred the apple slices in the unmarked wrapper. If you're using a binomial test to determine whether the children show a particular preference for the apple slices in one of the wrappers, what is the null hypothesis? \( \mathrm{H}_{0}: \mathrm{p}=\mathrm{p} \) (prefer apple slices in unmarked wrapper) \( >0.5 \) \( \mathrm{H}_{0}: \mathrm{p}=\mathrm{p} \) (prefer apple slices in marked wrapper) \( <0.5 \) \( \mathrm{H}_{0}: \mathrm{p}=\mathrm{p} \) (prefer apple slices in unmarked wrapper) \( \neq 0.5 \) \( \mathrm{H}_{0}: \mathrm{p}=\mathrm{p} \) (prefer apple slices in unmarked wrapper \( )=0.5 \) The z-score for the number of children who preferred the apple slices in the unmarked wrapper is Use the Distribution tool to answer the following questions. The z-score for the number of children who preferred the apple slices in the unmarked wrapper is Use the Distribution tool to answer the following questions. marked wrapper \( )=0.5 \), the chi-square test statistic would be. If \( a=0.05 \), the decision is to the null hypothesis and you conclude the children have a preference for the unmarked wrapper.