(Solved): 6. Centre of Mass. The coordinates \( (\bar{x}, \bar{y}) \) of the centre of ...

???????

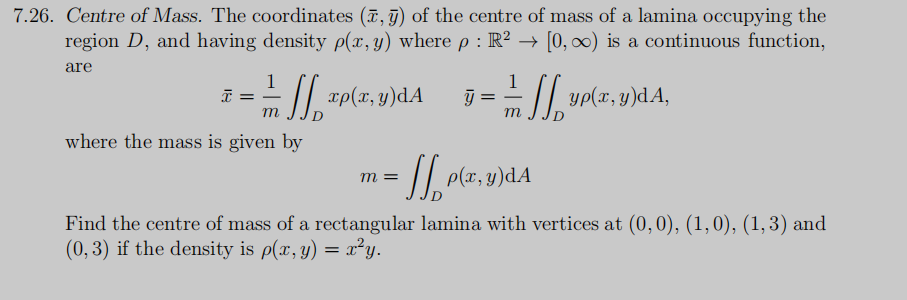
6. Centre of Mass. The coordinates \( (\bar{x}, \bar{y}) \) of the centre of mass of a lamina occupying the region \( D \), and having density \( \rho(x, y) \) where \( \rho: \mathbb{R}^{2} \rightarrow[0, \infty) \) is a continuous function, are \[ \bar{x}=\frac{1}{m} \iint_{D} x \rho(x, y) \mathrm{d} A \quad \bar{y}=\frac{1}{m} \iint_{D} y \rho(x, y) \mathrm{d} A, \] where the mass is given by \[ m=\iint_{D} \rho(x, y) \mathrm{d} A \] Find the centre of mass of a rectangular lamina with vertices at \( (0,0),(1,0),(1,3) \) and \( (0,3) \) if the density is \( \rho(x, y)=x^{2} y \).