(Solved): 5.2 The Uniform Distribution Definition - The uniform distribution is a continuous probability di ...

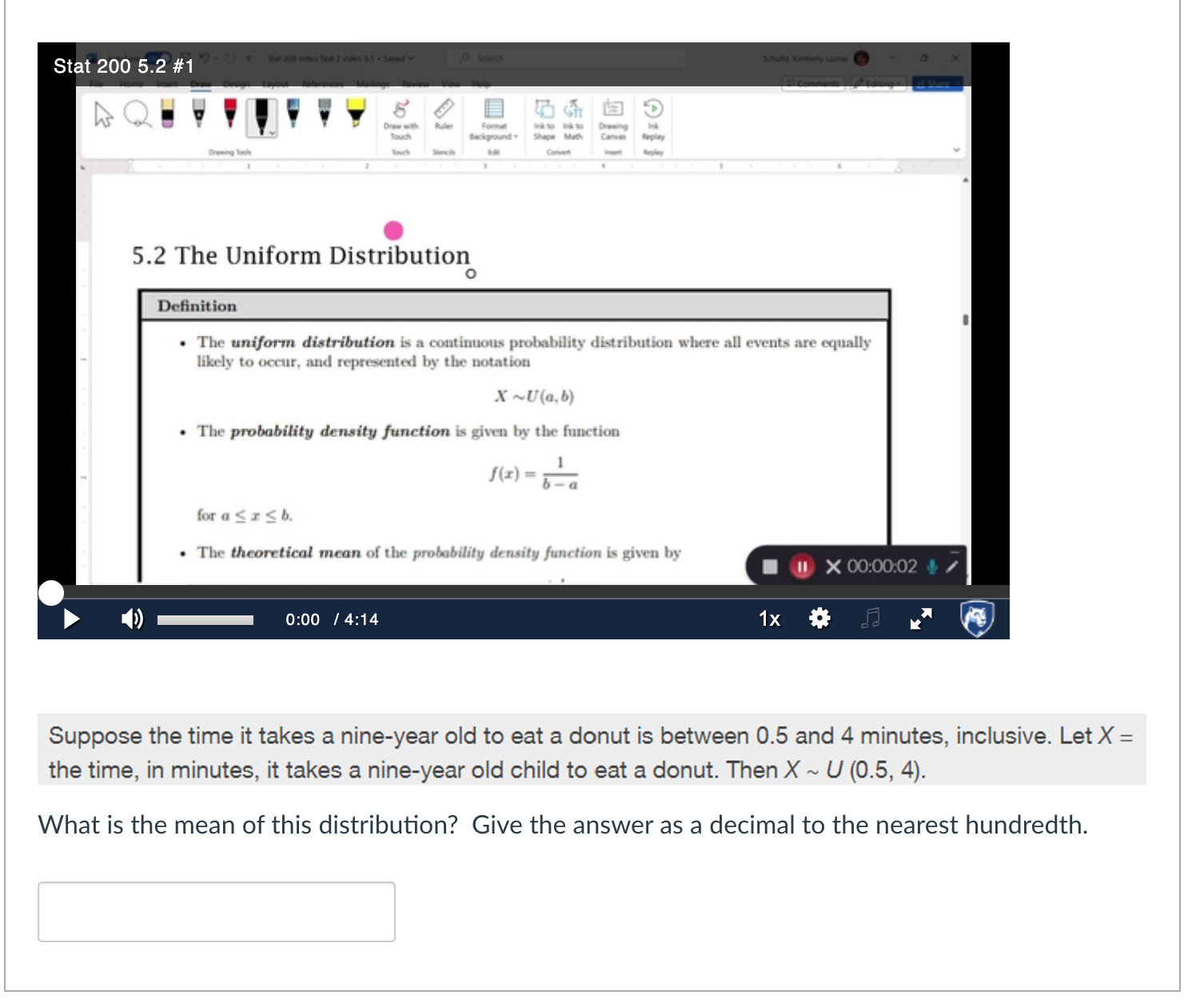
5.2 The Uniform Distribution Definition - The uniform distribution is a continuous probability distribution where all events are equally likely to occur, and represented by the notation $X?U(a,b)$ - The probability density function is given by the function $f(x)=\frac{1}{b?a}$ for $a?x?b$. - The theoretical mean of the probability density function is given by II) $\times 00:00:02$ (b) $0:00/4:14$ $1\times$ Suppose the time it takes a nine-year old to eat a donut is between 0.5 and 4 minutes, inclusive. Let $X=$ the time, in minutes, it takes a nine-year old child to eat a donut. Then $X?U(0.5,4)$. What is the mean of this distribution? Give the answer as a decimal to the nearest hundredth. 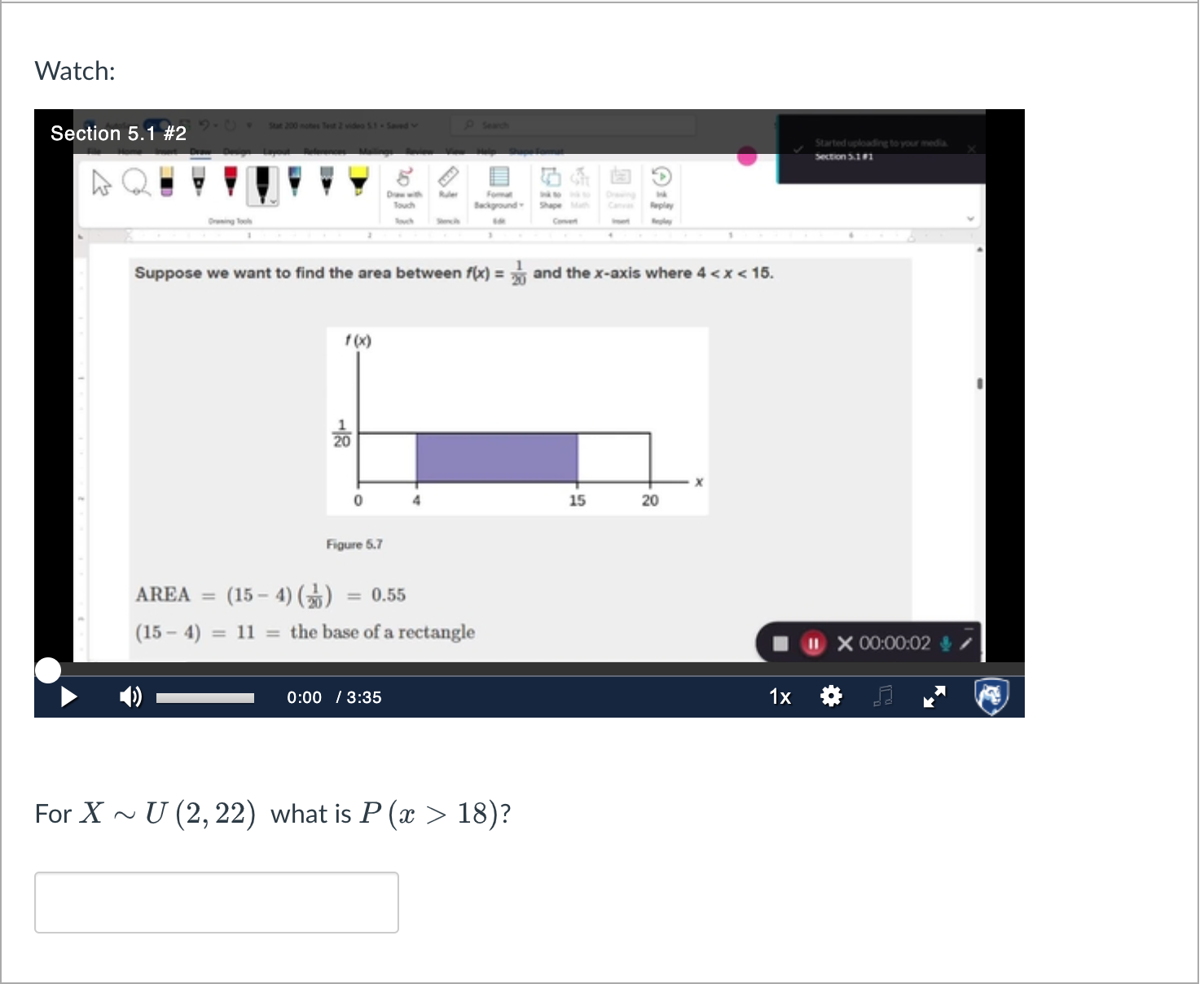Suppose we want to find the area between $f(x)=\frac{1}{20}$ and the $x$-axis where $4<x<15$. Figure 5.7 AREA $=(15?4)\left(\frac{1}{20}\right)=0.55$ $(15?4)=11=$ the base of a rectangle For $X?U(2,22)$ what is $P(x>18)$ ? Suppose the time is takes en pe-year old to eat a donut is between 0.5 and 4 minutes, inclusive. Let $X=$ the time, in minutes, it takes a nine-year old child to eat a donut. Then $X?U(0.5,4)$. Problem a. The probability that a randomly selected nine-year old child eats a donut in at least two minutes is b. Find the probability that a different nine-year old child eats a donut in more than two minutes given that the child has already been eating the donut for more than 1.5 minutes. The swcond question has a conditional probability. You are asked to find the probability that a nineyear old child eats a donut in more than two minutes given that the child has already been eating the donut for more than 1.5 minutes. Solve the problem two dilferent ways (see You must reduce the sample space. First way. Since you know the child has already been eating the donut for more than 1.5 minutes, you are no longer starting at $a=0.5$ minutes. Your starting point is 1.5 minutes. Write a new $f(x)$ : $\begin{array}{l}f(x)=\frac{1}{4?15}=\frac{2}{5}\text{ for }1.5?x?4.\\ \text{ Find }P(x>2?x>1.5)\text{. Draw a graph. }\end{array}$ $0:00/7:03$ $1\mathrm{x}$ Assume that $X?U(2,27)$ what is $P(5<x<10)$. Glve your answer as a decimal. 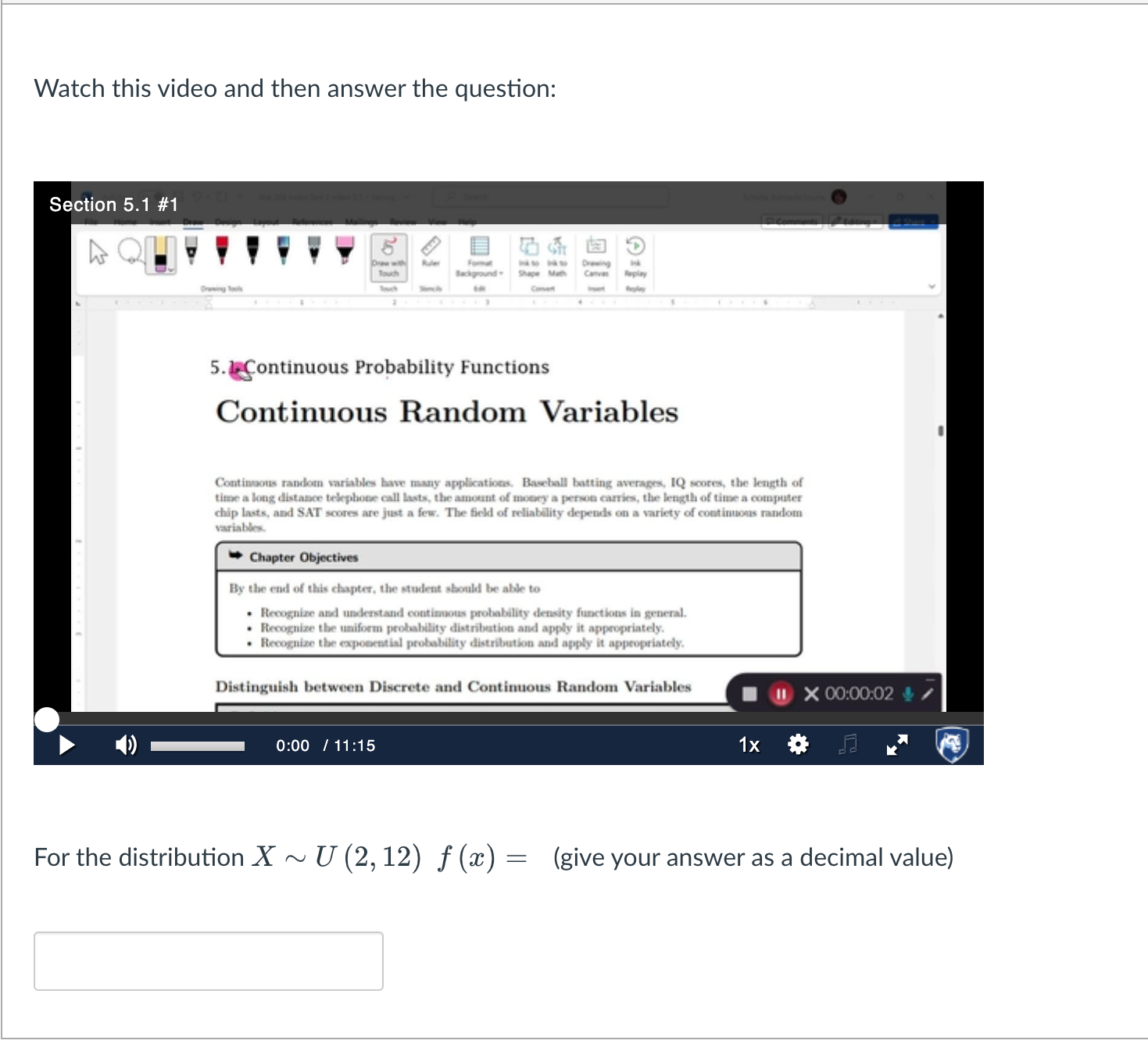Watch this video and then answer the question: Section $5.1\#1$ Onewey low 5. Lefontinuous Probability Functions Continuous Random Variables Continoous random variables bave many applicatioes. Baveball batting averages, IQ voores, the length of time a lotig distasere tekphose call lasts, the amount of moesy a pernoe carries, the length of time a computer chip lasts, and SAT scores are just a few. The field of reliability depends on a variety of continuons random variables. Chapter Objectives By the end of this chapter, the strulent sbould be able to - Recognixe asd understand contimoous probability density functions in general. - Recognixe the uniform probability distribution and apply it appropriately. - Recognise the expoecential probability distribution and apply it appeopriately. Distinguish between Discrete and Continuous Random Variables 0) 0:00/11:15 (11) $\times 00:00:02$ For the distribution $X?U(2,12)f(x)=$ (give your answer as a decimal value)