(Solved): 49 and 53 please Theory and Examples In Exercises 49-54, show that the limits do not exist. 49. \( \ ...

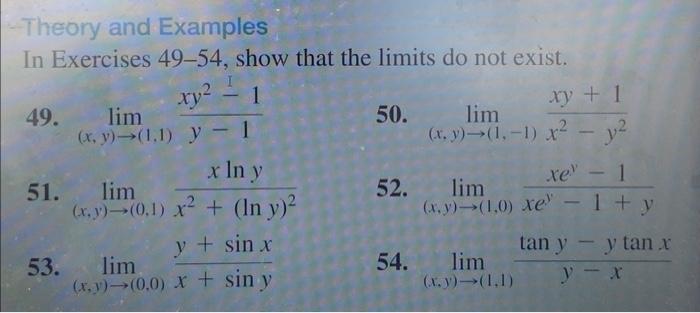
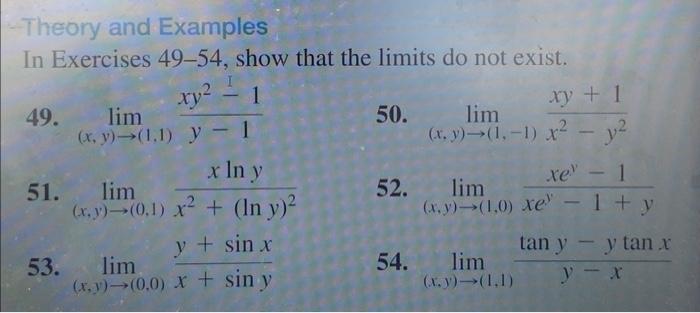
Theory and Examples In Exercises 49-54, show that the limits do not exist. 49. \( \lim _{(x, y) \rightarrow(1,1)} \frac{x y^{2}-1}{y-1} \) 50. \( \lim _{(x, y) \rightarrow(1,-1)} \frac{x y+1}{x^{2}-y^{2}} \) 51. \( \lim _{(x, y) \rightarrow(0,1)} \frac{x \ln y}{x^{2}+(\ln y)^{2}} \) 52. \( \lim _{(x, y) \rightarrow(1,0)} \frac{x e^{y}-1}{x e^{y}-1+y} \) 53. \( \lim _{(x, y) \rightarrow(0,0)} \frac{y+\sin x}{x+\sin y} \) 54. \( \lim _{(x, y) \rightarrow(1,1)} \frac{\tan y-y \tan x}{y-x} \)