(Solved): 4 and 5 please 4. Using Euler's relation, \( e^{j \theta}=\cos \theta+j \sin \theta \), derive the e ...

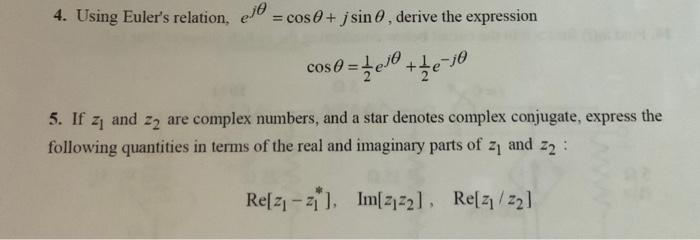
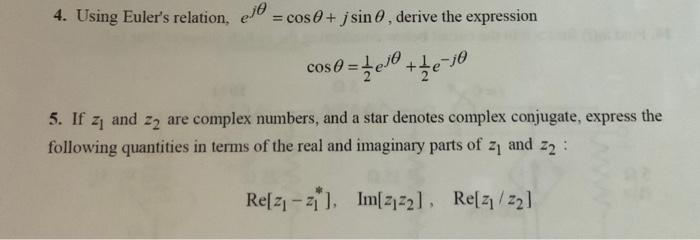
4. Using Euler's relation, \( e^{j \theta}=\cos \theta+j \sin \theta \), derive the expression \[ \cos \theta=\frac{1}{2} e^{j \theta}+\frac{1}{2} e^{-j \theta} \] 5. If \( z_{1} \) and \( z_{2} \) are complex numbers, and a star denotes complex conjugate, express the following quantities in terms of the real and imaginary parts of \( z_{1} \) and \( z_{2} \) : \[ \operatorname{Re}\left[z_{1}-z_{1}^{*}\right], \quad \operatorname{Im}\left[z_{1} z_{2}\right], \quad \operatorname{Re}\left[z_{1} / z_{2}\right] \]