(Solved): 34 Consider the satellite-attitude control problem shown in Fig. \( 4.45 \) where the normalized ...

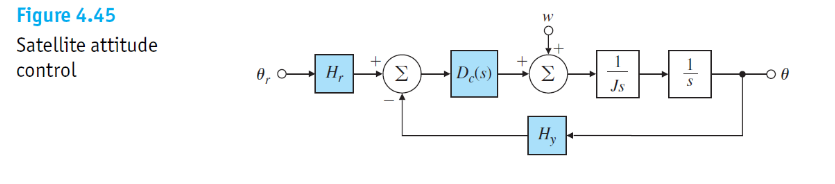
34 Consider the satellite-attitude control problem shown in Fig. \( 4.45 \) where the normalized parameters are \( J=10 \quad \) spacecraft inertia, \( \mathrm{N} \cdot \mathrm{m} \cdot \mathrm{sec}^{2} / \mathrm{rad}^{2} \) \( \theta_{r}= \) reference satellite attitude, rad. \( \theta= \) actual satellite attitude, rad. \( H_{y}=1 \quad \) sensor scale, factor \( \mathrm{V} / \mathrm{rad} \). \( H_{r}=1 \quad \) reference sensor scale factor, \( \mathrm{V} / \mathrm{rad} \). \( w= \) disturbance torque, \( \mathrm{N} \cdot \mathrm{m} \). a) Use proportional control, \( \mathrm{P} \), with \( D_{c}(s)=k_{P} \), and give the range of values for \( k_{P} \) for which the system will be stable. b) Use PD control, let \( D_{c}(s)=\left(k_{P}+k_{D} s\right) \), and determine the system type and error constant with respect to reference inputs. (c) Use PD control, let \( D_{c}(s)=\left(k_{P}+k_{D} s\right) \), and determine the system type and error constant with respect to disturbance inputs. d) Use PI control, let \( D_{c}(s)=\left(k_{P}+\frac{k_{I}}{s}\right) \), and determine the system type and error constant with respect to reference inputs. Figure 4.45 Satellite attitude control