(Solved): 2. Write an equation for the signals plotted in Figure 1 using ramp, unit step, and impulse functio ...

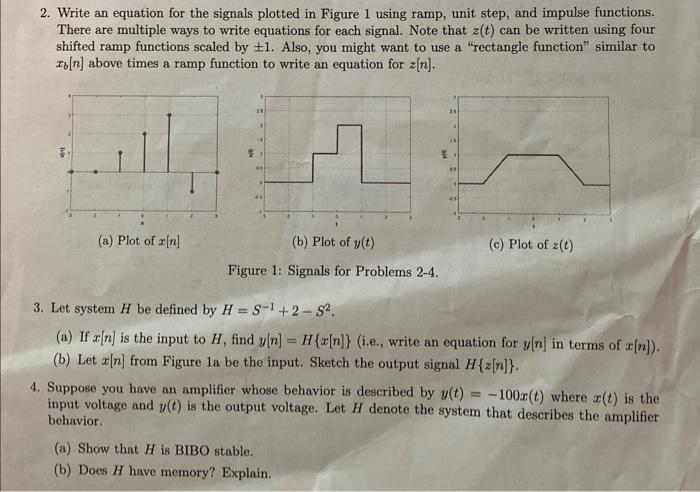
2. Write an equation for the signals plotted in Figure 1 using ramp, unit step, and impulse functions. There are multiple ways to write equations for each signal. Note that \( z(t) \) can be written using four shifted ramp functions scaled by \( \pm 1 \). Also, you might want to use a "rectangle function" similar to \( x_{b}[n] \) above times a ramp function to write an equation for \( z[n] \). (c) Plot of \( z(t) \) Figure 1: Signals for Problems 2-4. 3. Let system \( H \) be defined by \( H=S^{-1}+2-S^{2} \). (a) If \( x[n] \) is the input to \( H \), find \( y[n]=H\{x[n]\} \) (i.e,, write an equation for \( y[n] \) in terms of \( x[n] \) ). (b) Let \( x[n] \) from Figure 1 a be the input. Sketch the output signal \( H\{z[n]\} \). 4. Suppose you have an amplifier whose behavior is described by \( y(t)=-100 x(t) \) where \( x(t) \) is the input voltage and \( y(t) \) is the output voltage. Let \( H \) denote the system that describes the amplifier behavior. (a) Show that \( H \) is BIBO stable. (b) Does \( H \) have memory? Explain. (c) Explain why \( H \) is causal. (d) Define the inverse system \( H^{-1} \). Do this by writing \( x(t) \) as a function of \( y(t) \). (c) Show that \( H \) is linear.