(Solved): 2. The figure shows the configuration of a two-bulb system joined by a small tube, containing diff ...

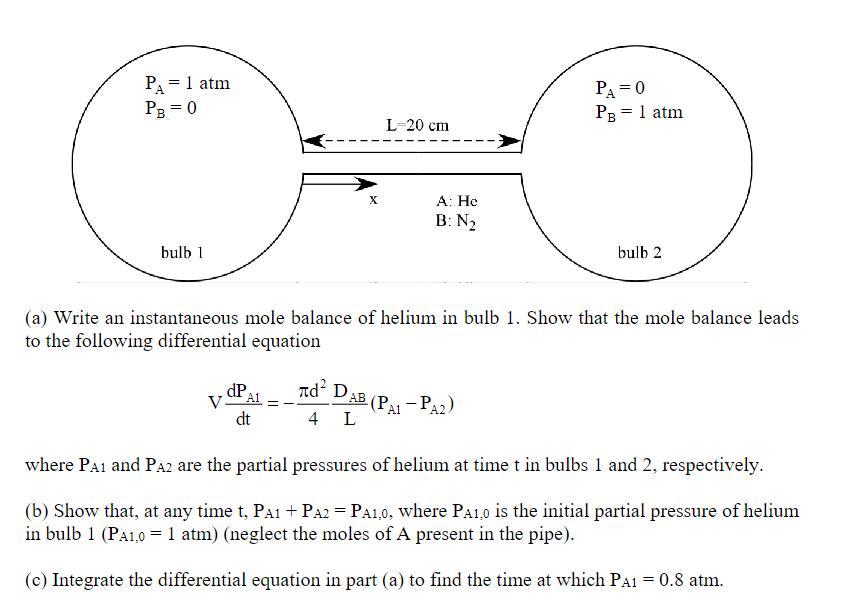
2. The figure shows the configuration of a two-bulb system joined by a small tube, containing different partial pressures of helium and nitrogen at \( \mathrm{t}=0 \). The two bulbs have the same volume, \( \mathrm{V}_{1}=\mathrm{V}_{2}=\mathrm{V}=1000 \mathrm{~cm}^{3} \), and the tube joining them has a length \( \mathrm{L}=20 \mathrm{~cm} \), and a diameter \( \mathrm{d}=2 \) \( \mathrm{cm} \). The system is at a constant temperature of \( 298 \mathrm{~K} \). The diffusivity in the binary mixture is \( \mathrm{D}_{\mathrm{AB}}=0.687 \mathrm{~cm}^{2} / \mathrm{s} \). We would like to estimate the time required for the partial pressure of helium in bulb 1 to drop to \( 0.8 \) atm. We will assume that the equimolar counterdiffusion process in the tube is at steady state at all times (pseudo-steady approximation). Check that moles in pipe are negligible. (a) Write an instantaneous mole balance of helium in bulb 1 . Show that the mole balance leads to the following differential equation where \( \mathrm{P}_{\mathrm{A} 1} \) and \( \mathrm{P}_{\mathrm{A} 2} \) are the partial pressures of helium at time \( t \) in bulbs 1 and 2 , respectively. (b) Show that, at any time t, \( \mathrm{P}_{\mathrm{A} 1}+\mathrm{P}_{\mathrm{A} 2}=\mathrm{P}_{\mathrm{A} 1,0} \), where \( \mathrm{P}_{\mathrm{A} 1,0} \) is the initial partial pressure of helium in bulb \( 1\left(\mathrm{P}_{\mathrm{A} 1,0}=1 \mathrm{~atm}\right) \) (neglect the moles of \( \mathrm{A} \) present in the pipe). (c) Integrate the differential equation in part (a) to find the time at which \( \mathrm{P}_{\mathrm{A} 1}=0.8 \mathrm{~atm} \).