(Solved): 2. Elasticity and total revenue The following graph shows the daily demand curve for bikes in Detro ...

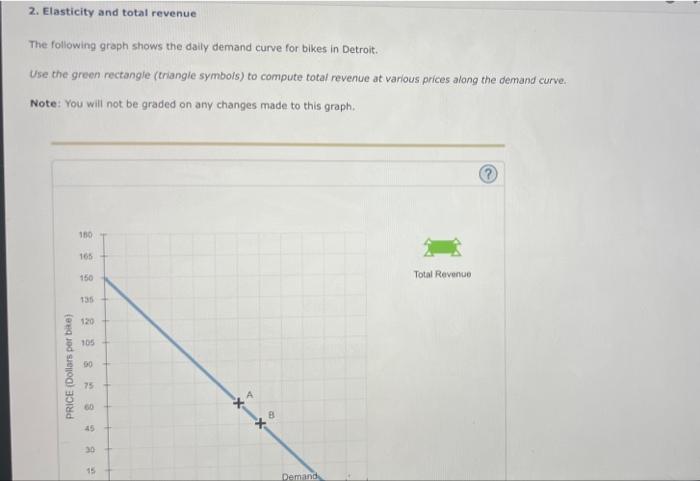
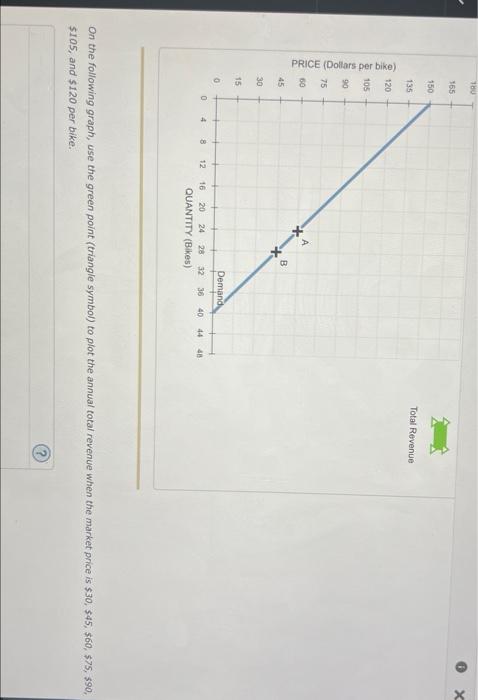
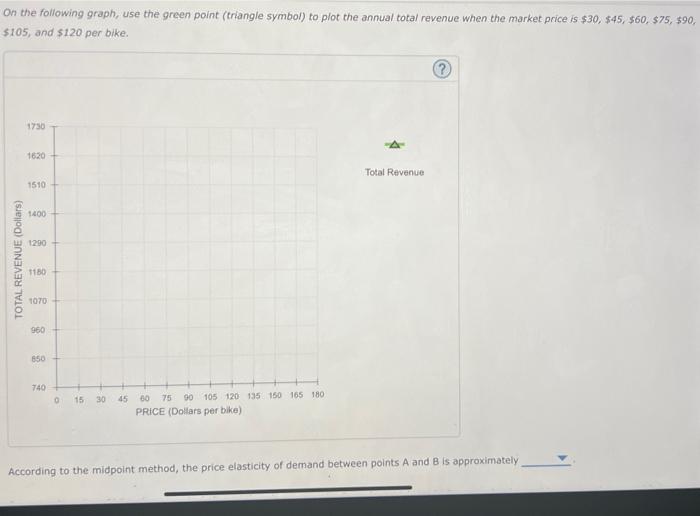
2. Elasticity and total revenue The following graph shows the daily demand curve for bikes in Detroit. Use the green rectangle (triangle symbols) to compute total revenue at various prices along the demand curve. Note: You will not be graded on any changes made to this graph. On the following graph, use the green point (triangle symbol) to plot the annual cotal revenue when the market price is \( \$ 30 \), \( \$ 45 \), \( \$ 60 \), \( \$ 75 \), \( \$ 90 \), \( \$ 105 \), and \( \$ 120 \) per bike. On the following graph, use the green point (triangle \( \$ y m b o l) \) to plot the annual total revenue when the market price is \( \$ 30 \), \( \$ 45 \), \( \$ 60 \), \( \$ 75 \), \( \$ 90 \), \( \$ 105 \), and \( \$ 120 \) per bike. 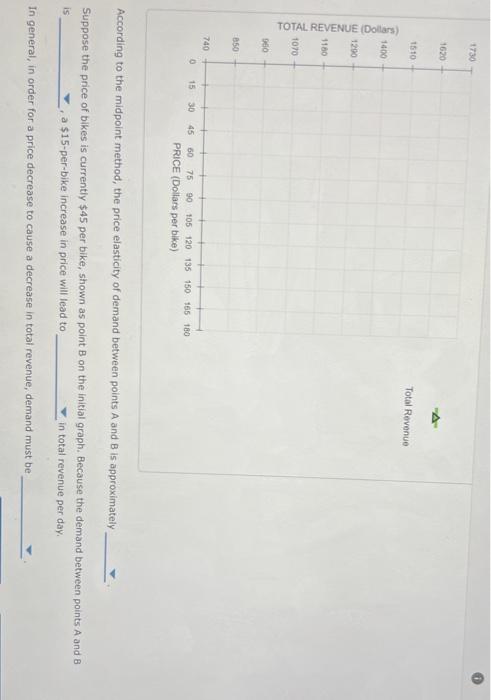According to the midpoint method, the price elasticity of demand between points \( \mathrm{A} \) and \( \mathrm{B} \) is approximately According to the midpoint method, the price elasticity of demand between points \( \mathrm{A} \) and \( \mathrm{B} \) is approximately Suppose the price of bikes is currently \( \$ 45 \) per bike, shown as point \( B \) on the initial graph. Because the demand between points \( A \) and \( B \) is a \$15-per-bike increase in price will lead to in total revenue per day. In general, in order for a price decrease to cause a decrease in total revenue, demand must be