(Solved): (2) Converting the decimal values to binary values of the correct size for each field: opcode \( = ...

(2) Converting the decimal values to binary values of the correct size for each field: opcode \( =11111000010 \), address \( =011110000 \), op \( =00, \quad \mathrm{Rn}=01010, \mathrm{Rt}=01001 \) opcode \( =10001011000, \mathrm{Rm}=01001, \quad \) shamt \( =000000, \mathrm{Rn}=10101, \mathrm{Rd}=01001 \) opcode \( =1001000100, \quad \) immediate \( =000000000001, \quad \mathrm{Rn}=01001, \mathrm{Rt}=01001 \) opcode \( =11111000000 \), address \( =011110000, \mathrm{op}=00, \quad \mathrm{Rn}=01010, \mathrm{Rt}=01001 \) R-type (ADD) and D-type (LDUR and STUR) instructions have 11-bit opcodes I-type instructions have 10-bit opcodes D-type address fields are 9 bit and D-type op fields are 2 bit I-type immediate fields are 12 bit R-type shamt fields are 6 bit Register fields (Rn, Rm, Rd, Rt) are always 5 bit 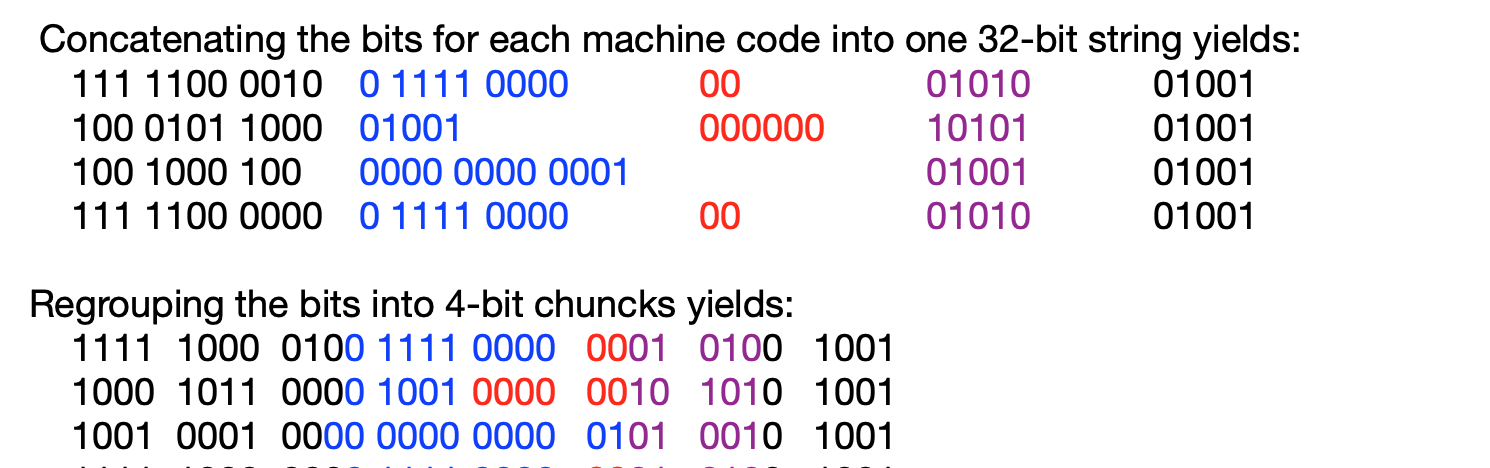Concatenating the bits for each machine code into one 32 -bit string yields: \( \begin{array}{lllll}11111000010 & 011110000 & 00 & 01010 & 01001 \\ 10001011000 & 01001 & 000000 & 10101 & 01001 \\ 1001000100 & 000000000001 & & 01001 & 01001 \\ 11111000000 & 011110000 & 00 & 01010 & 01001\end{array} \) Regrouping the bits into 4-bit chuncks yields: \( 11111000010011100000001 \quad 0100 \quad 1001 \) \( \begin{array}{lllllll}1000 & 1011000010010000 & 0010 & 1010 & 1001\end{array} \) \( 10010001000000000000 \quad 0101 \quad 0010 \quad 1001 \)