(Solved): 1. Theoretical Analysis of RC Circuit Using Phasors The circuit shown in Figure 1 will be analysed ...

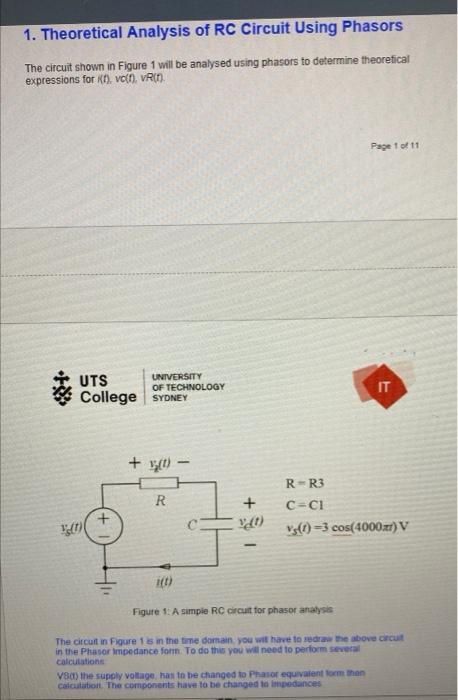
1. Theoretical Analysis of RC Circuit Using Phasors The circuit shown in Figure 1 will be analysed using phasors to determine theorefical expressions for \( (f) \), vo(f), vR(f) Pegel of 11 \begin{tabular}{l|l} \( 4.4 \) UTS & UNIVERSTY OF TECHNOLOGY SYDNEY \\ \( \mathrm{R}=\mathrm{R} 3 \) \\ \( \mathrm{C}=\mathrm{Cl} \) \\ \( \mathrm{v}_{\mathrm{S}}(t)=3 \cos (4000 \pi t) \mathrm{V} \) \end{tabular} Figure 1: A simple RC circut for phasor anatysis The cifcuit in Fygure 1 is in the time damain. you wit have to redran the above crcul in the Phasor impedance form. To do ther you will need to perform several colculations V8(i) the supply vollage, has to be changed to Piasor equivarent torm than caicialation. The components have to be charged to limpedances calculation. The components have to be changed to Impedances. 2.1 Determine Zeq and i(t) - Write the value of the voltage phasor Vs Vs \( = \) - Use the formula \( \mathrm{Zc}=-j \mathrm{j} \omega \mathrm{C} \) to calculate the impedance of the capacitor \( \mathrm{Zc} \) \( Z_{c}= \) - Noting that the resistor and capacitor are in series, determine the equivalent impedance Zeq in rectangular form. \( Z_{\text {eq }}= \) - Draw these components of impedance in the complex plane axes and determine Zeq in polar form. \( Z_{\text {eq }}= \) (Polar form) - Use Ohm's law to solve for the phasor current 1 in the circuit. I = Vs I Zeq (Remember that to divide a phasor by a complex number, divide the magnitudes and subtract the phase angle.) \( 1= \) - Write the time domain expression for \( i(t) \) \( i(t)= \) 2.2 Determine \( v_{c}(t) \) - Use Ohm's law to solve for the phasor voltage Vc across the capacitor, \( V c=1 x \) \( \mathrm{Zc} \) (Remember that to multiply a phasor by a complex number, multiplythe magnitudes and add the phase angle.) \( V_{s}= \) - Write the time domain expression for \( V_{c}(t) \) \( V_{e}(t)= \) \( 2.3 \) Determine \( v_{R}(t) \) - Use Ohm's Law to solve for the phasor voltage \( V_{R} \) across the resistor. \( V_{R}=1 \times R \) \( V_{R}= \) - Write the time domain expression for \( V_{n}(t) \). \( V_{n}(f)= \) 2.4 Sketch the phasor diagram for \( V_{a}, V_{0}, V_{n} \)