Home /
Expert Answers /
Mechanical Engineering /
1-the-rod-assembly-has-a-mass-per-unit-length-of-3kg-m-and-is-rotating-with-a-constant-angular-v-pa557
(Solved): 1) The rod assembly has a mass per unit length of 3kg/m and is rotating with a constant angular v ...
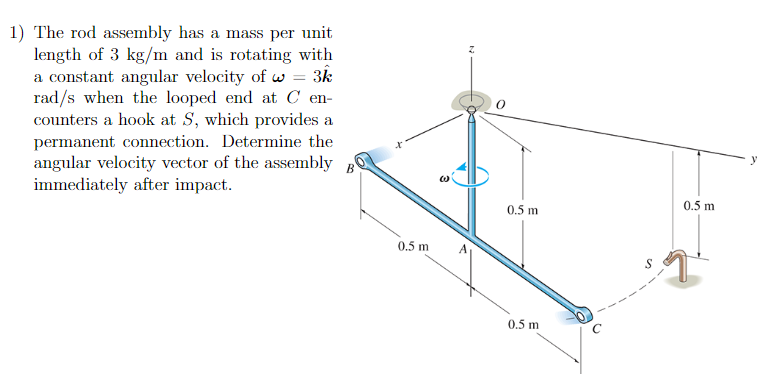
1) The rod assembly has a mass per unit length of and is rotating with a constant angular velocity of when the looped end at encounters a hook at , which provides a permanent connection. Determine the angular velocity vector of the assembly immediately after impact.
Expert Answer
To determine the angular velocity vector of the assembly immediately after impact, we can use the principle of conservation of angular momentum, which states that the total angular momentum of a system remains constant if no external torque acts on the system.Before the impact, the assembly has zero angular velocity since it is at rest. After the impact, the assembly will start rotating due to the collision. Let's assume that the direction of rotation is counterclockwise, which means that the angular velocity vector will point upward out of the page.To calculate the magnitude of the angular velocity vector, we can use the principle of conservation of energy, which states that the total energy of a system remains constant if no external forces act on the system. In this case, the initial potential energy of the mass is converted into kinetic energy of both the mass and the assembly, as well as rotational kinetic energy of the assembly. Therefore, we can write: where m is the mass of the ball, h is the initial height of the ball, v is the velocity of the ball just before impact, I is the moment of inertia of the assembly, and ? is the angular velocity of the assembly just after impact.We can solve for ? to get: where d is the distance between the axis of rotation and the center of mass of the assembly. Note that we assume the ball sticks to the assembly after the impact.The direction of the angular velocity vector is counterclockwise, which means that it points upward out of the page.