(Solved): 1. The following IPE300 rolled-steel beam is subjected to two forces as shown in the figure. Determ ...

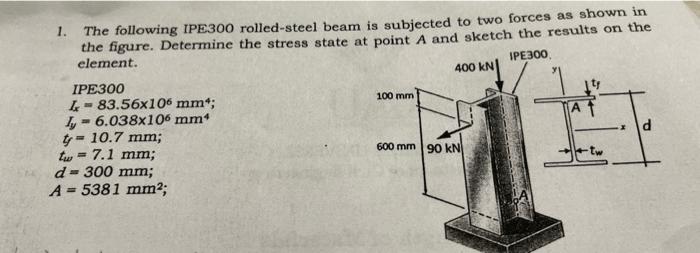
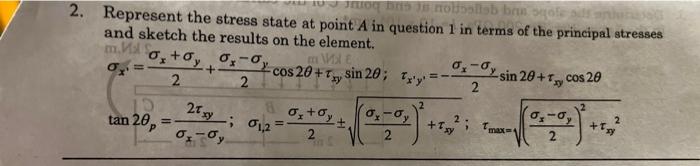
1. The following IPE300 rolled-steel beam is subjected to two forces as shown in the figure. Determine the stress state \( a^{t} \) nnint \( A \) and sketch the results on the element. \[ \begin{array}{l} I P E 300 \\ I_{x}=83.56 \times 10^{6} \mathrm{~mm}^{4} \\ I_{y}=6.038 \times 10^{6} \mathrm{~mm}^{4} \\ t_{f}=10.7 \mathrm{~mm} \\ t_{w}=7.1 \mathrm{~mm} \\ d=300 \mathrm{~mm} \\ A=5381 \mathrm{~mm}^{2} \end{array} \] Represent the stress state at point \( A \) in question 1 in terms of the principal stresses and sketch the results on the element. \( \sigma_{x^{\prime}}=\frac{\sigma_{x}+\sigma_{y}}{2}+\frac{\sigma_{x}-\sigma_{y}}{2} \cos 2 \theta+\tau_{x y} \sin 2 \theta ; \quad \tau_{x^{\prime} y^{\prime}}=-\frac{\sigma_{x}-\sigma_{y}}{2} \sin 2 \theta+\tau_{x y} \cos 2 \theta \) \( \tan 2 \theta_{p}=\frac{2 \tau_{x y}}{\sigma_{x}-\sigma_{y}} ; \quad \sigma_{1,2}=\frac{\sigma_{x}+\sigma_{y}}{2} \pm \sqrt{\left(\frac{\sigma_{x}-\sigma_{y}}{2}\right)^{2}+\tau_{x y}^{2}} ; \quad \tau_{\max }=\sqrt{\left(\frac{\sigma_{x}-\sigma_{y}}{2}\right)^{2}+\tau_{x y}^{2}} \)