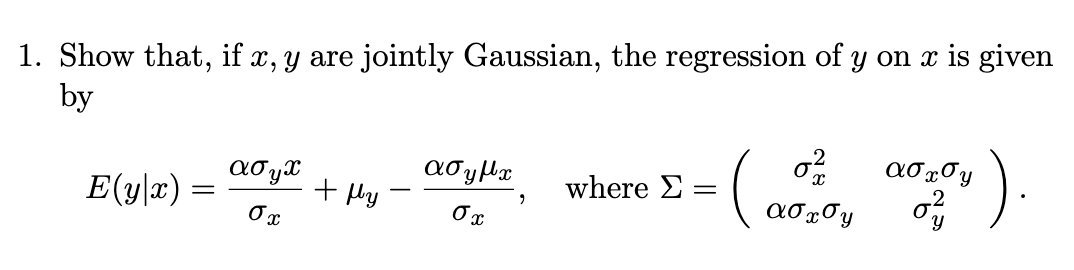(Solved): 1. Show that, if \( x, y \) are jointly Gaussian, the regression of \( y \) on \( x \) is given by ...

1. Show that, if \( x, y \) are jointly Gaussian, the regression of \( y \) on \( x \) is given by \[ E(y \mid x)=\frac{\alpha \sigma_{y} x}{\sigma_{x}}+\mu_{y}-\frac{\alpha \sigma_{y} \mu_{x}}{\sigma_{x}}, \quad \text { where } \Sigma=\left(\begin{array}{cc} \sigma_{x}^{2} & \alpha \sigma_{x} \sigma_{y} \\ \alpha \sigma_{x} \sigma_{y} & \sigma_{y}^{2} \end{array}\right) \]