(Solved): (1 point) The rectangles in the graph below illustrate a left endpoint Riemann sum for \( f(x)=\fr ...

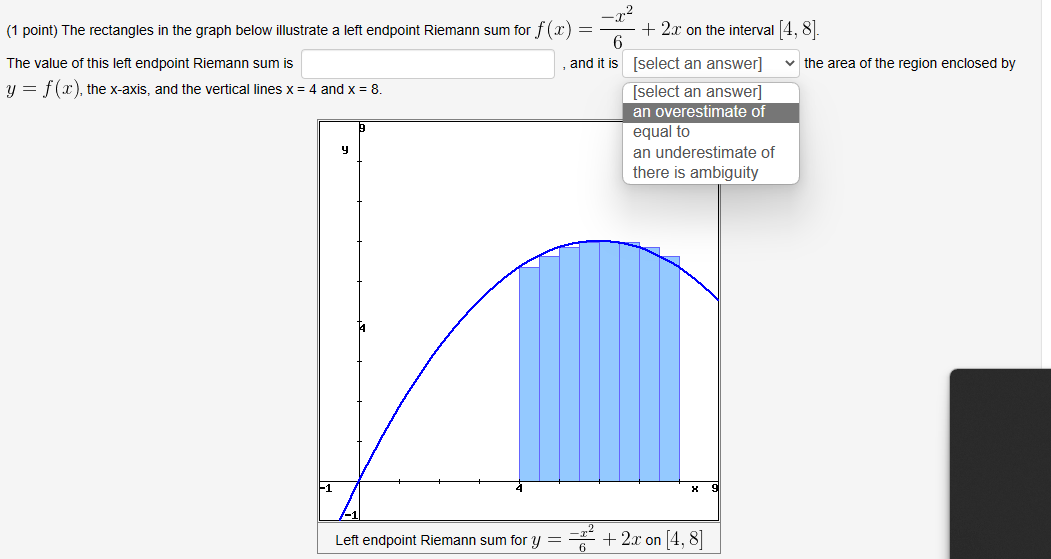
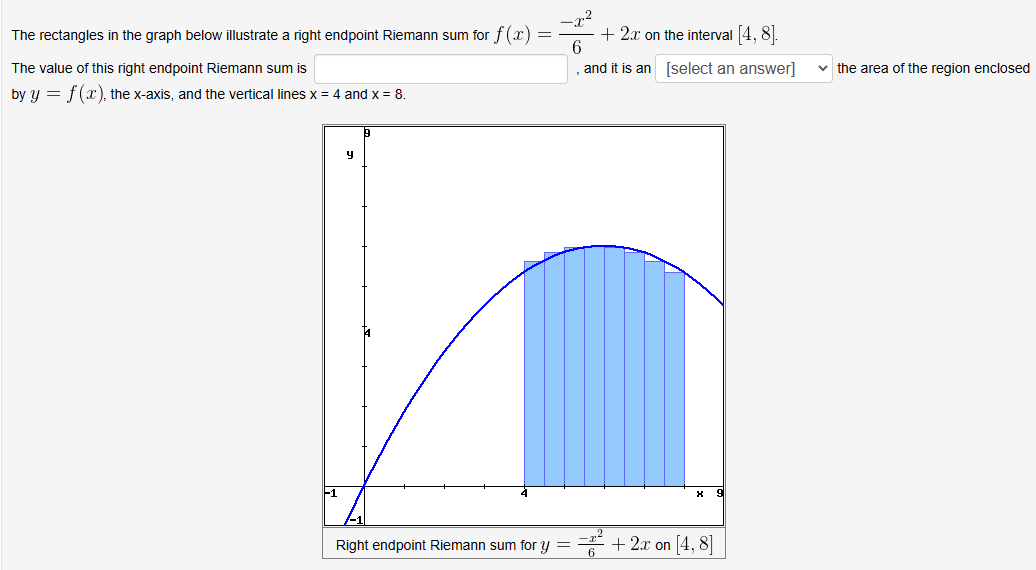
(1 point) The rectangles in the graph below illustrate a left endpoint Riemann sum for \( f(x)=\frac{-x^{2}}{6}+2 x \) on the interval \( [4,8] \). The value of this left endpoint Riemann sum is and it is the area of the region enclosed by \( y=f(x) \), the \( x \)-axis, and the vertical lines \( x=4 \) and \( x=8 \). The rectangles in the graph below illustrate a right endpoint Riemann sum for \( f(x)=\frac{-x^{2}}{6}+2 x \) on the interval \( [4,8] \). The value of this right endpoint Riemann sum is and it is an the area of the region enclosed by \( y=f(x) \), the \( \mathrm{x} \)-axis, and the vertical lines \( \mathrm{x}=4 \) and \( \mathrm{x}=8 \). Using left and right Riemann sums based on the diagrams above, we definitively conclude that \[ \begin{array}{l} \leq \int_{4}^{6} \frac{-x^{2}}{6}+2 x d x \leq \\ \leq \int_{6}^{8} \frac{-x^{2}}{6}+2 x d x \leq \\ \leq \int_{4}^{8} \frac{-x^{2}}{6}+2 x d x \leq \end{array} \] Hint: For the last integral, you should consistently choose either to underestimate or overestimate the area. This may require that you use the left Riemann sum for some \( x \)-intervals and the right Riemann sum for other \( x \)-intervals.