(Solved): 1. As shown in Fig. 1, consider a two-dimensional steady irrotational flow of an inviscid and inco ...

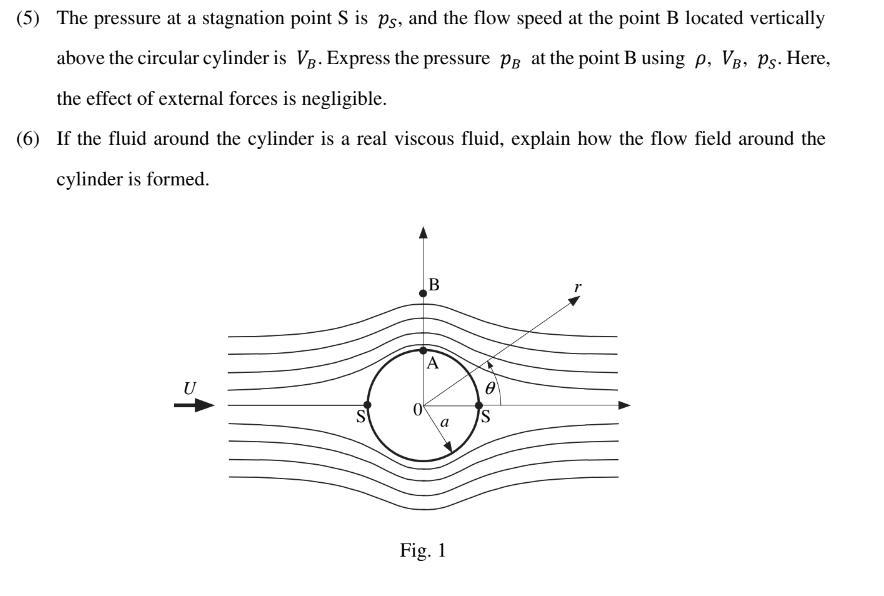
1. As shown in Fig. 1, consider a two-dimensional steady irrotational flow of an inviscid and incompressible fluid of density \( \rho \) around a circular cylinder. The radial and circumferential coordinates in the polar coordinate system are \( r \) and \( \theta \), respectively. The radius of the cylinder is \( a \), and the velocity of a uniform stream far from the cylinder is \( U \). The complex potential \( W(z) \) of this flow is given by \[ W(z)=U\left(z+\frac{a^{2}}{z}\right), \] where \( z=r e^{i \theta} \) is a complex variable in the polar form. Answer the following questions. (1) The above complex potential is expressed by a superposition of multiple flow fields. Explain the flow fields with describing each complex potential. (2) Express the velocity potential \( \phi(r, \theta) \) and the stream function \( \psi(r, \theta) \). Here, at the point A \( (a, \pi / 2) \) in the polar coordinates on the circular cylinder, \( \phi=0 \) and \( \psi=0 \). In addition, using a figure, explain the streamlines when \( \psi(r, \theta)=0 \). (3) Express the radial velocity \( V_{r} \) and the circumferential velocity \( V_{\theta} \). (4) Obtain the radial velocity \( V_{r} \) and the circumferential velocity \( V_{\theta} \) at the point \( \mathrm{A}(a, \pi / 2) \). (5) The pressure at a stagnation point \( S \) is \( p_{S} \), and the flow speed at the point B located vertically above the circular cylinder is \( V_{B} \). Express the pressure \( p_{B} \) at the point \( \mathrm{B} \) using \( \rho, V_{B}, p_{S} \). Here, the effect of external forces is negligible. (6) If the fluid around the cylinder is a real viscous fluid, explain how the flow field around the cylinder is formed. Fig. 1