(Solved): 1-7 please!!!!! 1-8 Find (a) the curl and (b) the divergence of the vector field. 1. \\( \\mathbf{F} ...

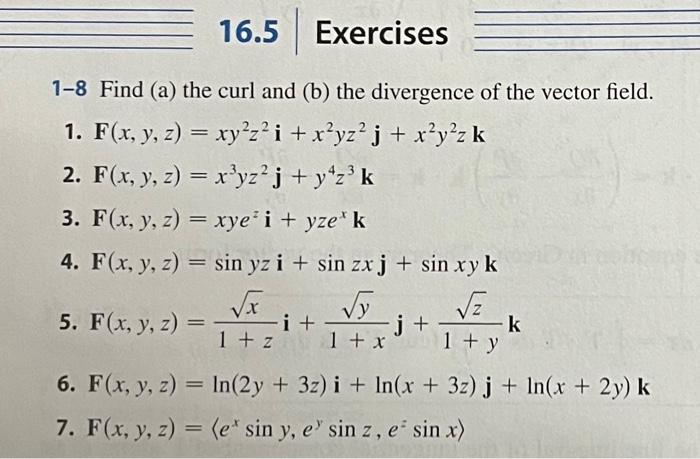
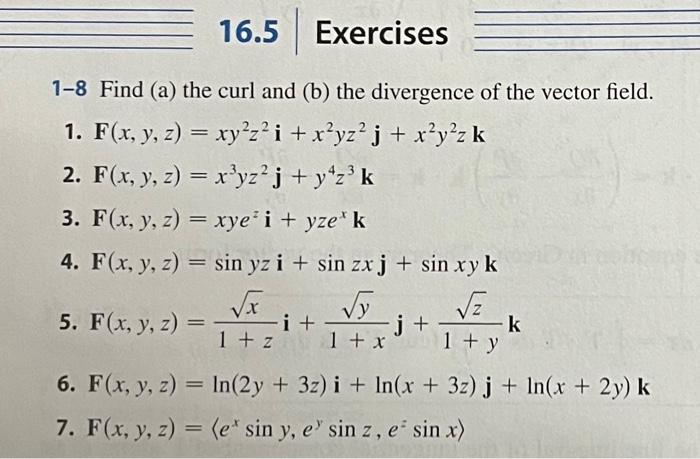
1-8 Find (a) the curl and (b) the divergence of the vector field. 1. \\( \\mathbf{F}(x, y, z)=x y^{2} z^{2} \\mathbf{i}+x^{2} y z^{2} \\mathbf{j}+x^{2} y^{2} z \\mathbf{k} \\) 2. \\( \\mathbf{F}(x, y, z)=x^{3} y z^{2} \\mathbf{j}+y^{4} z^{3} \\mathbf{k} \\) 3. \\( \\mathbf{F}(x, y, z)=x y e^{z} \\mathbf{i}+y z e^{x} \\mathbf{k} \\) 4. \\( \\mathbf{F}(x, y, z)=\\sin y z \\mathbf{i}+\\sin z x \\mathbf{j}+\\sin x y \\mathbf{k} \\) 5. \\( \\mathbf{F}(x, y, z)=\\frac{\\sqrt{x}}{1+z} \\mathbf{i}+\\frac{\\sqrt{y}}{1+x} \\mathbf{j}+\\frac{\\sqrt{z}}{1+y} \\mathbf{k} \\) 6. \\( \\mathbf{F}(x, y, z)=\\ln (2 y+3 z) \\mathbf{i}+\\ln (x+3 z) \\mathbf{j}+\\ln (x+2 y) \\mathbf{k} \\) 7. \\( \\mathbf{F}(x, y, z)=\\left\\langle e^{x} \\sin y, e^{y} \\sin z, e^{z} \\sin x\\right\\rangle \\)